Breeding Register Machines

Continued from “(Almost) evolving Artificial Chemistries”

In review

Wolfgang Banzhaf and Christian Lasarczyk presented a mind-blowing paper at a workshop I attended back in 2004, called “Genetic Programming of an Algorithmic Chemistry”. The premise here was so weird to most of us in the audience (I suspect) that while we were totally amazed, we also totally didn’t manage to get our heads around just what they were demonstrating. Viz: They could evolve functional, useful machine learning models in a programming language in which the steps are run in random order.

Over the last few hours (four days, actually, in my time, but the coding is maybe 3 hours’ work total so far) I’ve tried to re-implement the system they describe. I’m working in Clojure, but that’s just because I have Clojure handy. It’s simple enough to be written in any modern language very very quickly. I’m calling one of these Artificial Chemistry/Random-sequence Programs a RegisterMachine, and yesterday Nic McPhee and I paired a little while and discovered some interesting overlaps with the UNITY system from the 1980s. Things are now at a point in the code I’ve developed where I can

1. Construct a random RegisterMachine like this, which I think is just like the ones described in the 2004 paper:

   (->RegisterMachine
     (into [] (repeatedly 11 #(- (rand 100.0) 50.0)))
     (into [] (repeat 30 0.0 ))
     (random-program all-functions 11 30 100))
   

2. “Run” that RegisterMachine for 500 steps, each time initializing it with one of the training cases from the target problem (where I’m asking it to approximate \(y=sin(x)\) with arithmetic operators only), and collect the resulting “error” values that compare the expected output for each training case to the observed output for that case:

   user=> (error-vector my-random-register-machine 500 sine-data)
   [0.10378827843255478 892.0499052239678 18.37429574385431 0.6847344424616899 1.902938338944094 17.607796834595234 64.72280429418238 77.93459127132203 1.7744408595140553 0.9999293957892215 0.9999220395963438 17.29715262620314 1.4737284487789573 1.9840846292005816 0.7243123524797839 23.77400340811076 1.1271712421646807 0.021030176634362685 1.6191202120650372 0.2910593407505375 0.9971295277731475 0.45038453426850644 0.8856534202977996 747.1416867968015 NaN 1031.555391958217 0.3721928299470263 0.07876230732670841 2.9720056901150205E-4 18.36661313122966 15.758647707960073 26.818799309181763 1.4797315826059496 1.2307856360961258 1.9819938312873038 25.148449574957457 0.01405532063619419 1.7352604176814883 0.003627605577099957 0.7034931593461528 1.54996967207728 18.478902850317226 1.2076058704811978 NaN 0.011615652574838764 0.45150998833643197 18.919854150630023 19.110623495653407 54.69284851926107 2.404829264973627E53 0.0719015045193675 1.7867418594573108 1.0080684465479774 54.23260103709737 17.51701096461205 19.070889990722012 0.5922074520335718 14.233090623213045 1.8490890527031547 1.2913604334427227 0.4162180977177288 45.78021083323095 17.138060672654525 0.7897811374963661 891.3624213797258 0.12341543902350127 17.882249298858323 0.6590661609510462 1.3175475027017796 0.8352648846255233 0.02005712202665677 17.774209879501168 1.621167494953838 0.7261127331940007 17.77898208232051 1.3421209214092846 17.559721083800202 1.9501932310889192 79.673881711732 17.958052184999275 1.4799155068769339 0.7235348717060249 1.0888954474194799 892.4454730534084 54.154566648044174 0.22562038124213035 17.737496622619393 18.19427576991408 18.60852670082341 0.9638079415516216 0.6928199029233504 64.19144649505957 0.9633289991749456 1.898821962863234 0.9933174578439989 0.4731621477855388 17.15104891080844 0.37258390769748145 0.026497669377493094 8.852097344403157]
   

That’s sort of performance information is what I need to start comparing different RegisterMachine instances against one another. And that is all we really need to start improving them.

Old-school mistakes

It was 2004 when the paper was written—more than a decade back—but even then, the authors were already starting to express regret over using a bad aggregated error statistic when comparing their evolved programs. Which is to say: I’ll use Mean Squared Error to begin with, because they did… but I won’t like it. But I’m trying to replicate their work, a little, so I need to at least go through the motions.

Don’t be like us, kids. Don’t use aggregated error scores for evolving, unless you know for a fact you have to.

I’ll do it this way, then we’ll do it a few other ways to clear the air, afterwards.

What Nic and I calculated in our error-vector yesterday is an ordered collection of absolute differences between expected and observed output values. Mean Squared Error (MSE) is just the sum of the squares of those, easy enough in Clojure, but presented here for completeness’ sake:

(defn mean-squared-error
  "Takes a collection of numeric values, squares them, adds those to produce a single sum"
  [numbers]
  (reduce + (map #(* %1 %1) numbers)))

(fact "mean-squared-error does what the sign says"
  (mean-squared-error [0 0 0 0 0 0]) => 0
  (mean-squared-error [0 0 0 0 0 1]) => 1
  (mean-squared-error [0 0 0 0 0 2]) => 4
  (mean-squared-error [2 2 2 2 2 2]) => 24
  )

Now I can score an arbitrary RegisterMachine’s MSE using

(mean-squared-error (error-vector my-register-machine 100 sine-data))

Make a few guesses

The worst we could possibly do at solving a problem like this is to sit and guess randomly until we get something we like. By which I mean: make a series of independent guesses, obstinately ignoring good and bad ones we’ve made in the past, just accumulating dice-rolls without trying to learn from the evaluations of the ones we’ve already done.

That’s an important thing to understand about all machine learning algorithms, evolutionary or not: The “placebo effect” to which you’re comparing your algorithmic treatment should always start with, “Does this algorithm tend to find answers better than an equivalent number of i.i.d. guesses?”

What does guessing give me? I decide to look at the MSE measurements for 10000 randomly-chosen RegisterMachine instances, all checked against the same sine-data values. Here’s a way of collecting some data, just to look quickly with another spreadsheet plot:

(dotimes [x 100]
    (let [rm (->RegisterMachine
               (into [] (repeatedly 11 #(- (rand 100.0) 50.0)))
               (into [] (repeat 30 0.0 ))
               (random-program all-functions 11 30 100))
          errs (error-vector rm 500 sine-data)]
      (spit
        "random-rms.csv"
        (str (clojure.string/join ", " (conj errs (mean-squared-error errs))) "\n")
        :append true)
        ))

Running that produces a file called random-rms.csv, containing a random sample of a hundred different RegisterMachine instances, and runs each of them 500 steps (per the protocol described in the book chapter) against each of 100 training cases. Just to get a better sense of what’s happening, I’ve saved both the MSE and all the 100 individual absolute error values.

It’s not a fast process, and I’m tempted already to parallelize it a bit and run it multithreaded. But I don’t want to do any premature optimization, and to be frank I see something else that might be more important to address first.

Here are the MSE values for these 1000 machines, sorted… “numerically” we’ll say:

1   53.6190999
2   53.6190999
3   53.6190999
4   78.79894709
5   83.13198742
6   88.41459029
7   93.13113577
8   93.27346612
9   100.8182265
10  112.6750623
11  114.237492
12  115.1560113
13  118.9073533
14  140.1020626
15  142.5843692
16  149.8582804
17  150.5917969
18  156.1441245
19  156.7875366
20  12082.30613
21  236943.5161
22  315744.6489
23  2367854.157
24  5012222.211
25  7897667.711
26  1.99E+07
27  6.17E+13
28  1.76E+15
29  1.71E+19
30  6.01E+19
31  1.57E+21
32  1.47E+59
33  9.86E+60
34  5.90E+122
35  6.06E+186
36  3.11E+247
37  1.61E+292
38  5.27E+303
39  Infinity
40  Infinity
41  Infinity
42  Infinity
43  Infinity
44  Infinity
45  Infinity
46  Infinity
47  Infinity
48  Infinity
49  Infinity
50  Infinity
51  Infinity
52  Infinity
53  Infinity
54  Infinity
55  Infinity
56  NaN
57  NaN
58  NaN
59  NaN
60  NaN
61  NaN
62  NaN
63  NaN
64  NaN
65  NaN
66  NaN
67  NaN
68  NaN
69  NaN
70  NaN
71  NaN
72  NaN
73  NaN
74  NaN
75  NaN
76  NaN
77  NaN
78  NaN
79  NaN
80  NaN
81  NaN
82  NaN
83  NaN
84  NaN
85  NaN
86  NaN
87  NaN
88  NaN
89  NaN
90  NaN
91  NaN
92  NaN
93  NaN
94  NaN
95  NaN
96  NaN
97  NaN
98  NaN
99  NaN
100 NaN

To summarize, there are 38 numerical results, 17 Infinity results, and 45 NaN results. The majority of the MSE scores are not numbers at all.

Remember when I was writing the arithmetic functions, and we ran across the problem of NaN results from exponentiation? Specifically, any exponentiation (or root, which is the same thing) that would produce a complex result, will instead produce a NaN result here. I said that seemed reasonable, because NaN is actually a well-behaved notion in the Clojure numerics world, and it’s contagious. So for example a calculation that ends up attempting (+ 9 NaN) will produce NaN as its result.

And that’s what’s happening here.

There are 45 out of 100 sampled NaN results for mean-squared-error, but there are only 236 instances of NaN in all those 10000 saved error scores combined. Remember, each of the mean-squared-error scores is the result of squaring and adding all 100 individual absolute error scores. Only 191 out of 10000 of those ended up being NaN, but those 191 are all contagious when we calculate MSE. In the vast majority of training cases, the programs that report NaN MSE scores had numerical error scores for all their other training cases.

Should I

1. filter out all NaN results from error-vector before calculating MSE?
2. disqualify all NaN results, essentially giving them the same score as the programs that return Infinity?
3. filter out the NaN results from error-vector, but also count how many failures there were, so we can penalize the programs that produce them in some other way later?
4. something else?

Here’s one of the lines from my data file, just to show you how rare these missteps seem to be:

14.512700656855618, 36.34682661832332, 0.22272076458235046, 36.0415438803616, 0.7028474400477173, 37.90569529133373, 3.4694618411003758E28, Infinity, 0.0049883792078943, 1.1430386388965226, 0.9764584409500819, 36.48257041838092, 17.699342124054212, 34.81858014561794, 35.268293081187856, 18.64664456285559, 20.312467626751573, 18.905021195269036, 18.79277331650665, 35.12632134580146, 160.58497171539184, 36.818180888782045, 1.0770428450393044, 3.211162515334249, 1.2774869325431761, 38.23513203047197, 4144.994254238535, 1.1205167681148849, 0.6517147658882435, 74.68681753890394, 8.089206762248192, 35.06506528509666, 158.45029664047635, NaN, 0.36017409166636516, 1.9882826305419015, 1.965103343683725, 17.09079339300167, 0.21610452505994493, 161.5178058457626, Infinity, 52.79181524968903, 11.416960575720818, 1.9985199759739016, 10.839149371903444, 6.902096518313083E-5, 0.473857988855935, 105.4739600503263, 48.7061839395908, 2.9773983899186405, 1.727524286383126, 2440.394926193592, 37.58780396402384, 37.131262078687215, 1.108107062748793, 2.9233951751453473, 16.38745019927218, 1.0010957494005623, Infinity, 1.8758971919377665, 0.8062492781324515, 20.63384160624596, 16.11828203393142, 0.4470185971167757, 36.00276024518086, 86.60253820111583, 34.15631844233021, 160.70700283399782, 141.5350108563254, 16.368476468845742, 36.99207386592062, 160.7608435407269, 18.16886154514844, 20.533004418208556, 70.46297145640446, 36.987484598558055, 30.403467871355716, 35.89971218150966, 26.341121061777525, 0.717927897631977, 263.21612142321567, 34.8079222070921, 37.99256501112781, 35.18023028374965, 15.838547544107891, 31.77076644759274, 19.095975690949597, 7.0124801295878816E106, 159.09327188544106, 25.10152924293739, 35.44651622632778, Infinity, 160.7983744944989, 0.7492663870031635, 15.10771712587888, 0.977449133958204, 161.69659912975297, 87.5916493382293, 17.34714203126965, 20.642120559459855, NaN

There are four Infinity values, but the final MSE (the last number in the line) is NaN because there was one NaN somewhere in the middle there. I’m frustrated because I can compare Infinity to other numbers, but NaN is not on a scale. But I’m also frustrated because there’s a lot of perfectly reasonable arithmetic going on in there, most of the time.

I suspect almost all of the RegisterMachine instances I’m running contain one or more NaN values somewhere, but recall we decided that the “output” was just the value of the last register of :connectors on the last step of execution. Machines that produce NaN in the course of execution, but keep it to themselves, I actually admire somewhat. In the same sense, I admire these machines that only rarely glitch out on the “output” value nearly as much. I want to give them a chance, in case most of the arithmetic they’re doing is somewhere close to a good answer.

I think I’ll pick option 3 from my list of options: I’ll filter out the NaN values, but also report how many of them there were. That way, I’ll get a numerical value for MSE, but can penalize the bad actors somehow, in case they start learning to just produce one pretty-good value and 99 refusals to cooperate.

Revised scores

Here’s a revised data-saving algorithm, which splits the scores in error-vector into two subsets (one entirely composed of NaN values), and returns an MSE score calculated over the numerical results, plus a count of non-numerical values:

  (dotimes [x 100]
    (let [rm (->RegisterMachine
               (into [] (repeatedly 11 #(- (rand 100.0) 50.0)))
               (into [] (repeat 30 0.0 ))
               (random-program all-functions 11 30 100))
          errs (error-vector rm 500 sine-data)
          bad  (filter isNaN? errs)
          good (filter #(not (isNaN? %)) errs)]
      (spit
        "random-rms.csv"
        (str (clojure.string/join 
                ", " 
                (conj good (mean-squared-error good) (count bad)))
             "\n")
        :append true
        )))

When I sort these numbers in a spreadsheet, it’s somehow a lot more pleasing to me to see a column of relatively small BAD values (the number of training cases that produce a result of NaN) and a column of entirely numerical GOOD results (the MSE calculated over the remaining training cases):

BAD   GOOD
0   53.6190999
0   53.6190999
0   53.6190999
0   53.6190999
1   58.4460994
0   78.84701251
0   97.01725554
0   110.2208883
0   116.3372093
0   127.6079183
0   132.0089151
0   134.7418056
0   136.1563229
0   138.842436
0   149.259414
0   155.824788
0   156.7703922
0   993.381172
1   13675.63454
0   48479.37548
0   83913.2372
0   101299.8314
0   172206.2436
0   236576.8369
0   256383.0347
0   317320.8615
0   349745.2179
3   4384612.192
0   5863468.618
0   2.24E+07
0   2.68E+07
0   4.62E+07
1   1.13E+08
2   1.42E+08
0   1.48E+08
0   2.20E+08
0   3.56E+08
0   9.61E+09
6   8.26E+17
0   2.61E+26
0   3.52E+26
0   4.51E+33
2   1.14E+70
3   7.48E+75
6   6.36E+84
0   1.83E+85
0   1.06E+103
5   2.89E+115
8   1.65E+146
3   7.03E+208
4   1.02E+212
1   1.84E+220
0   4.47E+268
0   1.77E+274
1   4.00E+274
1   2.42E+287
5   Infinity
3   Infinity
3   Infinity
0   Infinity
1   Infinity
2   Infinity
0   Infinity
1   Infinity
0   Infinity
4   Infinity
9   Infinity
4   Infinity
2   Infinity
1   Infinity
1   Infinity
8   Infinity
0   Infinity
3   Infinity
10  Infinity
2   Infinity
11  Infinity
1   Infinity
9   Infinity
10  Infinity
0   Infinity
1   Infinity
0   Infinity
0   Infinity
2   Infinity
0   Infinity
0   Infinity
2   Infinity
2   Infinity
3   Infinity
1   Infinity
1   Infinity
0   Infinity
3   Infinity
7   Infinity
4   Infinity
3   Infinity
1   Infinity
1   Infinity
2   Infinity

Everybody’s got a number, even if it’s Infinity. That’s OK with me, because I can sort Infinity.

I think I can live with this. The idea, in case it’s not obvious, is to compare two RegisterMachine instances on the basis of both their “failures” and “error”. That is, minimize the mean-squared-error over the numerical results they produce, and also minimize the number of non-numerical results they produce. We’ll see what happens.

But I’d better make it official, first! Here’s a clojure function that implements that filtering, and returns a hash with two key-value pairs in it. I can use that later to actually score RegisterMachine examples.

(defn errors-and-failures
  "Takes a RegisterMachine and a bunch of training cases, runs the machine for each case, collects the error-vector, and returns two scores: the MSE of all numerical results, and the count of non-numerical results"
  [rm steps data]
  (let [errs (error-vector rm steps data)
        bad  (filter isNaN? errs)
        good (filter #(not (isNaN? %)) errs)]
      {:mse (mean-squared-error good) :failures (count bad)}
    ))

To be honest, I’m comfortable for the moment just minimizing the numerical error, and ignoring those bad non-numerical results for now.

Better and better

Guessing only gets one so far. Also, guessing and then evaluating each with a calculation that takes at least 50000 iterations (100 training cases, 500 steps to run each program) is surprisingly boring, at least until it starts to pay off. Let’s make the search algorithm a little bit smarter.

The original paper (PDF) describes two search operators:

Mutation will change operator and register numbers according to a probability distribution. In the present implementation register values are changed using a Gaussian with mean at present value and standard deviation 1.

I’m reading this, plus the values reported in Table 11-1, to mean that

1. for each :read-only register, the numerical value stored there is changed, with probability 0.03, to a new random Gaussian number with mean equal to the old number, and variance equal to 1.0
2. for each number appearing in either the :args or :target fields of a ProgramStep in the machine, there is a 0.03 chance of changing it to another valid number, using the same approach used to initialize them; that is, :args value are any integer value up to the total number of registers in the machine, and :target numbers are any integer value up to the total number of :connectors registers

Note that nothing is said about mutating the function present. The only thing mutation affects is the numerical constants stored in :read-only, and the connections feeding into and out of the functions already present.

Functions themselves are modified by recombination (aka “crossover”).

1. each :read-only register value is copied with equal probability from either parent
2. …?

I can’t suss out what they actually did for crossover between the programs here. It reads as if there was a last-minute change before the manuscript was submitted, because there’s something about “sequence generators” and stuff that doesn’t seem to have much to do with running these machines. Indeed, I begin to suspect that this whole experiment is framed in the authors’ minds as a comparison between Linear GP and this weird randomly-shuffled program execution style.

I have to guess what exactly they meant, in other words. That’s pretty normal, when you try to replicate results from any published paper. At least when the code isn’t included.

There’s a good deal of discussion about how the occurrence of a ProgramStep in an offspring depends on the frequency of occurrence in the “sequence generator” of the parent. That makes me think what is happening here is something like “pick 100 i.i.d. samples of ProgramStep entries, with replacement, from both parents”. But there’s also a suggestion (because of a “Maximum Size” entry in Table 11-1) that crossover between two same-length individuals can produce longer offspring.

I think what I’ll do is this:

1. call the two parents Mom and Dad
2. pick two integers: one a random integer between 0 and the length of Mom, and the other a random integer between 0 and the length of Dad
3. sample from Mom and Dad, randomly and with replacement, according to those numbers
4. construct the offspring’s program in whatever order you want (concatenation is as good as any)

Whew. Now I can implement some stuff.

Crossover first

I will save you the rather uneventful writing of the crossover functions. Here are the tests I wrote, in the end:

(fact "crossover-registers"
  (let [mom (->RegisterMachine [1 1 1 1] [0 0 0] [:a :b :c :d])
        dad (->RegisterMachine [2 2 2 2] [0 0 0] [:z :y :x :w])]
    (crossover-registers mom dad) => [1 2 1 2]
    (provided (rand) =streams=> [0 1 0 1])
    ))

(fact "crossover-program"
  (let [mom (->RegisterMachine [1 1 1 1] [0 0 0] [:a :b :c :d])
        dad (->RegisterMachine [2 2 2 2] [0 0 0] [:z :y :x :w])]
    (crossover-program mom dad) => [:MOM :MOM :MOM :DAD :DAD :DAD]
    (provided (rand-int 4) => 3
              (rand-nth [:a :b :c :d]) => :MOM
              (rand-nth [:z :y :x :w]) => :DAD
              )))

(fact "crossover"
  (let [mom (->RegisterMachine [1 1 1 1] [0 0 0] [:a :b :c :d])
        dad (->RegisterMachine [2 2 2 2] [0 0 0] [:z :y :x :w])]
    (crossover mom dad) => (->RegisterMachine
                              [1 2 1 2]
                              [0 0 0]
                              [:MOM :MOM :MOM :DAD :DAD :DAD])
    
    (provided (rand-int 4) => 3
              (rand-nth [:a :b :c :d]) => :MOM
              (rand-nth [:z :y :x :w]) => :DAD
              (rand) =streams=> [0.1 0.8 0.1 0.8])))

Thank goodness (again) for Brian Marick’s Midje testing framework. I especially like the way I can use a “streaming prerequisite” like (rand) =streams=> [...] to stub a random function out but still have it produce a deterministic sequence of different values.

And here is the final library code that makes these tests pass:

(defn crossover-program
  "Takes two RegisterMachines. Randomly samples some ProgramSteps from each, returning a new program combining the samples"
  [mom dad]
  (let [mom-program (:program mom)
        mom-contrib (rand-int (count mom-program))
        dad-program (:program dad)
        dad-contrib (rand-int (count dad-program))]
    (into [] (concat
      (repeatedly mom-contrib #(rand-nth mom-program))
      (repeatedly dad-contrib #(rand-nth dad-program))
      ))))

(defn crossover-registers
  "Takes two RegisterMachines. Constructs a new `:read-only` vector by sampling from the two with equal probability."
  [mom dad]
  (map #(if (< (rand) 1/2) %1 %2) (:read-only mom) (:read-only dad)))

(defn crossover
  "Takes two RegisterMachines, and does crossover of both their `:read-only` vectors and programs"
  [mom dad]
  (->RegisterMachine
    (crossover-registers mom dad)
    (:connectors mom)
    (crossover-program mom dad)))

I’ve broken out the two aspects of crossover described in the paper into two separate functions, one of which constructs a new :read-only vector of constants, and the other which builds a new collection of ProgramStep items for the offspring.

Giving it a try

I want to see this thing work, in the sense that I want to see improvement over time happening right in front of me. I’m going to make an executive decision here, and implement a much simpler search algorithm than the old-fashioned stuff described in the paper.

What I’m about to implement, just to have some positive feedback after a couple of days’ worth of typing these long rambling accounts, is called a steady-state evolutionary algorithm. Well, it’s one kind of steady-state algorithm.

Here’s what I’ll do:

1. make a pile of random RegisterMachine dudes
2. run and evaluate all of them, producing (and recording inside them) their error and failure scores
3. pick two at random, with uniform probability
4. make an offspring from those, and evaluate it
5. discard the worst-scoring RegisterMachine from the pile, and replace it with the offspring I just made
6. GO TO step 3

I expect, over time, to see the score tend downwards. At least that’s what I hope.

One thing I do to make my life easier is probably something you’d also do if you were working in Javascript: Whenever I evaluate a RegisterMachine, I’ll just write its scores right into it, so I can keep better track of things as we go.

Fast forward

The short version of what happened next is: I spent a half-hour writing a mostly good—emphasis on the qualifier “mostly” here—ad hoc implementation of that search algorithm I just described. It seemed in most cases to run fine, but now and then it would crash with a mysterious OutOfBoundsException (or words to that effect). I’m happy considering it a design spike, and am about to throw it away.

The point of telling you this is twofold, I think: First, as much as I like telling you about the thought processes going on in my head when I’m learning about these systems I’m building, I know you don’t appreciate being dragged down into an interminable rat-hole of debugging and looking for typos. Second, it’s actually an excellent idea to work through a spike solution and throw it away before you actually start coding the “real thing”, in a mindful way. It opens up prospects, and closes off bad options with a lot less risk than you’d experience if you just started changing the core of a project without knowing even the sorts of thing you might end up needing to do.

For example, here are some of the things I observed, and while I may not stumble across them again as I develop a “real” version, I’m also glad I have a recent reminder. So I can, you know, be mindful:

An error error

There’s an amusing trick hidden in my choice of “minimize Mean Squared Errors” as a goal, which I’m almost 100% sure we’ll come across again now. By “trick” I mean a trick the system plays on me. This one I’ll save for when it comes up again in practice, but as a preview: Can you think of a simple way for a RegisterMachine to minimize the MSE scores, if it has 100 training cases, but only the ones that return numbers contribute to the MSE value…?

Crossover by dilution

There’s something extremely odd about the way recombination is done in this system, and I think I’ve read the paper correctly. By “odd” I mean, “Contrary to my experiences with regular programming languages, even GP ones.” Recall I’m taking two RegisterMachine programs, and picking a number of lines from each, at random and with replacement, then putting those piles into one pile in the “offspring”. And also recall that when we run a RegisterMachine program, we’re picking lines at random, with replacement. When mom and dad contribute stuff, often what they contribute is not a fair sample of what they can do.

This is a good place for an example. Say we apply crossover to two very different parents. When we run each parent, we get a random sequence of steps, and when we cross them over, we also use a random sequence of steps to decide what is carried over to baby. Let me show you what mom and dad produce on sampling, and then make a baby just by taking a block of stuff directly from those same “traces”:

mom: [1 2 3 4 5 6 7 8] ;; run => (5 2 1 2 1 6 7 7 7 1 3 2 1 8 3 3 3 3 3 5...)
                                  ^^^^^^^^^^^
dad: [11 22 33 44 55 66 77 88] ;; run => (11 77 77 22 88 88 11 11 55 66 33 77 33 33 88 88 22 33 77 77...)
                                          ^^^^^^^^^^^^^^^^^

baby: [5 2 1 2 1 6 11 77 77 22 88 88] => (22 1 88 6 1 77 77 22 77 88 77 1 77 1 88 77 88 77 77 1...)
       M M M M M M D  D  D  D  D  D

I picked 6 items from each of mom and dad here, but it might have been anywhere from zero to all of them. Note also that what I’ve shown as “genes” in my diagram are just integers, and if these were RegisterMachine parents we’d be talking about ProgramStep items that read and write register values. Do you notice something about the effects of this crossover? A lot is missing in the offspring. The baby lacks all of [3 4 7 8 33 44 55 66].

Now look how this plays out when mom and dad are much more similar to one another. Say they’re closely related; let’s say baby meets a close relative (whose genes I picked from the 6 items at the ends of the traces of mom and dad):

mom2: [5 2 1 2 1 6 11 77 77 22 88 88] => (22 1 88 6 1 77 77 22 77 88 77 1 77 1 88 77 88 77 77 1...)
dad2: [3 3 3 3 3 5 88 88 22 33 77 77] => (3 77 3 3 3 3 3 88 5 33 77 3 3 22 3 3 3 77 77 5...)

Notice anything about the numbers that are left in these? There are an awful lot of 3 and 77 and 88 here. Odds are high that their offspring will be 3-ing all over the place, when they run their programs. And as a result, their offspring will tend to be even more 3-ish, and so on.

So while Wolfgang and Christian discuss the fact that this representation is about concentrations of behaviors, I think it might be more important than just a metaphor. This canalization—a strong sampling error—is going to have a potent influence on the dynamics of search. Just as certain numbers disappeared from my lists above, some program steps will disappear and others will be duplicated, and at the same time the sizes of the programs is fluctuating randomly in a rather counterintuitive way. In other words, it might be the case that programs need to be long, in order to avoid introducing sampling errors among their offspring that would make them much more variable in behavior. That sort of side-effect makes me frown.

A constant source of innovation is important

Let’s just say that what I watched in my preliminary runs of my buggy code made me realize that some source of new program steps is going to be crucial, because of that drift thing I just mentioned. It could be a sort of mutation, changing the connections and functions of individual instructions, or it could just be the constant introduction of new individuals.

And here we go

Barbara paired with me a bit yesterday, while I was working through my design spike and watching numbers scroll by in the shell, since both of them are approximations with no known optimal solution. She wondered why I was using the problems described in the paper for testing, and I admit that’s a very good question. Whenever I teach or mentor people building a new GP system (of any sort), I always have them check that it can handle symbolic regression on \((y=x+6)\). That is, we provide a bunch of numbers x, and for each we want (+ x 6) as an output.

Yes, it’s trivial. That’s the point.

So here’s some new training data to use for that, picking 100 random x values between -50 and 50, and building training cases like the ones Nic and designed for \(y=sin(x)\):

(defn random-x6-case
  []
  (let [x (+ (rand 100) -50)]
    [[x] (+ x 6)]
    ))

(def x6-data
  (repeatedly 100 random-x6-case))

I’ll need some kind of “starting population” (what I called a “pile”) in my sketch above. These can be just like the RegisterMachine described in the paper; no reason to change that now:

(defn random-register-machine
  "Takes a function set, and counts of `:read-only` and `connectors` registers. All registers are set to 0.0"
  [function-set read-only connectors]
  (->RegisterMachine
    (into [] (repeat read-only 0.0))
    (into [] (repeat connectors 0.0))
    (random-program function-set read-only connectors)
    ))

There also needs to be some way to set the “evolved constants” here. Those are numbers we’ll write into :read-only when a new, random RegisterMachine is “born”, and never change unless we’re using them to make a new “baby” by crossover or mutation. But… we have no guidance in the paper for what range of values to use. I suppose we could start at 0.0, and let mutation work its way to wherever it wants to be. But that seems onerous; seems like it’d just be polite to give them something to work with.

Might as well be close to 0.0. Here’s a function to randomly assign values to the :read-only registers, given a numeric scale. It picks random numbers in the range [-range, range].

(defn randomize-read-only
  "Takes a RegisterMachine, and a range value, and sets each of the `:read-only` registers to a uniform random value between [-range, range]"
  [rm scale]
  (let [how-many      (count (:read-only rm))
        double-range  (* 2.0 scale)]
    (assoc rm
           :read-only
           (into [] (repeatedly how-many #(- (* (rand) double-range) scale)))
           )))

With that I can fiddle around with the relative scale of these constants, if I want to.

Make a pile of random dudes

Now I’ll want to be able to make and score a random pile, step 1 of my sketch above. I think I’ll work more interactively with this part, until I get it all put together.

Here I make a small pile (just 20 RegisterMachines), and then score it with the record-errors function Nic and I wrote the other day

(def starting-pile
  (repeatedly 
    20 
    #(randomize-read-only
      (random-register-machine all-functions 11 30 100)
        10
        )))

(println 
  (map :mse 
    (map #(record-errors % 20 x6-data) starting-pile)))

;; => (78316.2748796858 8653217.595852595 78708.54182364167 79392.55238697332 78696.6959863465 78572.68496379511 78148.85527597727 Infinity 78308.74922600105 78572.68496379511 78793.24927035745 75699.77797406889 78572.68496379511 78572.68496379511 Infinity 78801.47126240827 78497.32511673278 78573.0514207663 78624.13444276452 84672.14685086964)

Now I said I wanted to pick two of these at random, make a baby by crossover, and evaluate that.

(defn steady-state-breed-one
  "Takes a collection of RegisterMachines. Returns one new crossover product"
  [pile]
  (let [mom  (rand-nth pile)
        dad  (rand-nth pile)]
    (crossover mom dad)
    ))

(println
  (:mse (record-errors (steady-state-breed-one starting-pile) 20 x6-data)))

;; => 86617.25280586528

Now I said I wanted to remove the worst-scoring RegisterMachine in the pile first, before adding in the baby. OK:

(defn steady-state-cull-one
  [pile]
  (butlast (sort-by :mse (shuffle pile))))

(fact "culling removes a highest-scoring from a pile"
  (count (map :mse scored-start-pile)) => 
    (inc (count (map :mse (steady-state-cull-one scored-start-pile))))
  (map :mse scored-start-pile) =>
    (contains (map :mse (steady-state-cull-one scored-start-pile))
      :in-any-order :gaps-ok )
    )

So the cycle for search is something like this:

(defn report-line
  [t pile]
  (println
    (str t ", "
      (clojure.string/join ", " (map :mse pile))
      )))

(loop [pile scored-start-pile
       step 0]
  (if (> step 100)
    (report-line step pile)
    (do
      (report-line step pile)
      (recur (one-steady-state-step pile 500 x6-data)
             (inc step))
             )))

I’ve added a little report-line function, because really what good is evolutionary computing unless you pipe a bunch of random numbers to STDOUT?

Here’s what the numbers look like:

As you can probably see, at least they’re going down over time. But I note already that this is not a fast process. This was creating an initial pile of 20 random RegisterMachines, and then another 100 crossover products. A total of 120. One should expect to see hundreds of thousands of evaluations, but we’re going to do that on my laptop, at least not using 100 training cases, and 500 steps of “running” a program for each of the training cases.

Also, the heat from the laptop fan is making my knees burn.

If I were more committed to this version, I’d probably spend some time making it run on a small cloud somewhere. But recall this is a looking to see test. The fact the numbers are dropping over time makes me confident enough that something might happen if I had a more reasonable scope of search, but I’m also going to tone down the aggressiveness of evaluation (500 steps, 100 cases) to… let’s say 20 cases—it’s only \(y=x+6\), recall—and 100 steps?

(loop [pile scored-start-pile
       step 0]
  (if (> step 1000)
    (report-line step pile)
    (do
      (report-line step pile)
      (recur (one-steady-state-step pile 100 (take 20 x6-data))
             (inc step))
             )))

Wow that is way faster. OK, and… hey, wouldja look at that. It solved the problem perfectly, in only 34 steps!

This is when you should be remembering that I mentioned there was a trick. Sadly, I have neglected to print out the errors or program of the best-performing individual here, so maybe I should do that now, instead of the population’s MSE scores. I’ve noticed that the “new baby” is being added at the front of the pile (because I used conj, and the pile is a Clojure seq), but the lowest-scoring :mse machine is in the second position, still. I’ll print out its :mse over time. While I’m at it, I’ll print its :failures, too.

(defn report-line
  [t pile]
  (let [winner (second pile)]
    (println
      (str t ", "
        (:mse winner) ", "
        (:failures winner)
        ))))

I know it’s a different outcome than the one I saw earlier where a “perfect” machine was found in only 34 steps (and it’s going to be different every time I run it), but it’s qualitatively the same:

Somewhere around 300 steps along, we start to see those “perfect” machines, the ones with 0 :mse scores. Like I warned you: these are “perfect” because they always return NaN results. When I wrote record-errors, I separated out the :error-vector into the numeric and NaN parts, and only used the former for tallying :mse scores.

When there are no numeric :error-vector entries, then the :mse is 0. And I’m culling “worst” RegisterMachines based only on :mse.

Multiple objectives

What I want isn’t just a RegisterMachine that produces an :mse score of 0.0. I want one that does it without cheating.

In other words—I guess—I want the minimum :mse and the minimum :failures values. There’s obviously a trade-off here. Maybe I could get away with adding them together?

Well, yes and no. Looking at the numbers reported for :mse and :failures, the former is in the tens of thousands, and the latter is 20 at most (because that’s how many training cases there are). I’d rather make sure there aren’t any failures, so how about adding them with weights?

To “use” this combined error measure for selection, I’ll want to modify the way the pile of RegisterMachine answers is sorted.

(defn steady-state-cull-one
  [pile]
  (butlast 
    (sort-by
      #(+ (:mse %) (* 100000 (:failures %)))
     (shuffle pile))))

That is, I’m sorting by the sum of :mse and 100000 times the number of :failures. To be honest, I hate when people do that, but in this exploratory setting it feels almost-justified.

I hate adding together scores like that for several reasons. First, because inevitably one ends up needing at least one “magic number”—an unnamed numerical constant—or a vector of those. Somebody has to “pick the weights”, and even if they are hand-tailored to a given problem, and even if they are made into named constants, they’re still constants. Another reason I hate them is that each problem is often different from the others. Imagine if I had looked at the scores, and seen that :failures was about the same size as the :mse values I saw? Would I have still used such a big weight? Other reasons for my reticence involve the hulls of high-dimensional data points, and I won’t burden you with them here. But it makes me feel bad to do this.

That said, it certainly makes a difference in the trace of “winner” scores:

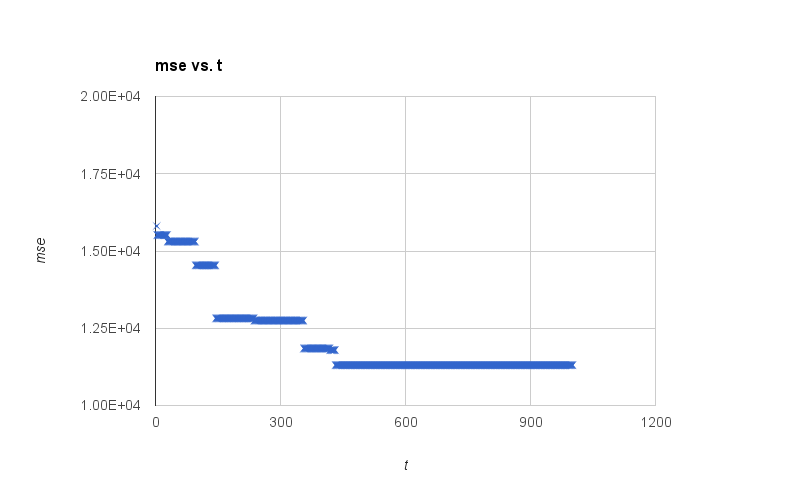
I suppose I need to look at the way the pile is changing as a whole, too. Along the way I’ve changed this little exploratory code back and forth a few times, so here’s the report-line and search loop I’m using right now:

(defn one-steady-state-step
  "Assumes the machines are scored before arriving"
  [pile steps data]
  (let [baby (record-errors (steady-state-breed-one pile) steps data)]
    (conj (steady-state-cull-one pile) baby)
    ))

(defn report-line
  [t pile]
  (println
    (str t ", "
      (clojure.string/join ", " (map :mse pile))
      )))

(loop [pile scored-start-pile
       step 0]
  (if (> step 1000)
    (report-line step pile)
    (do
      (report-line step pile)
      (recur (one-steady-state-step pile 100 (take 20 x6-data))
             (inc step))
             )))

And here’s what’s produced

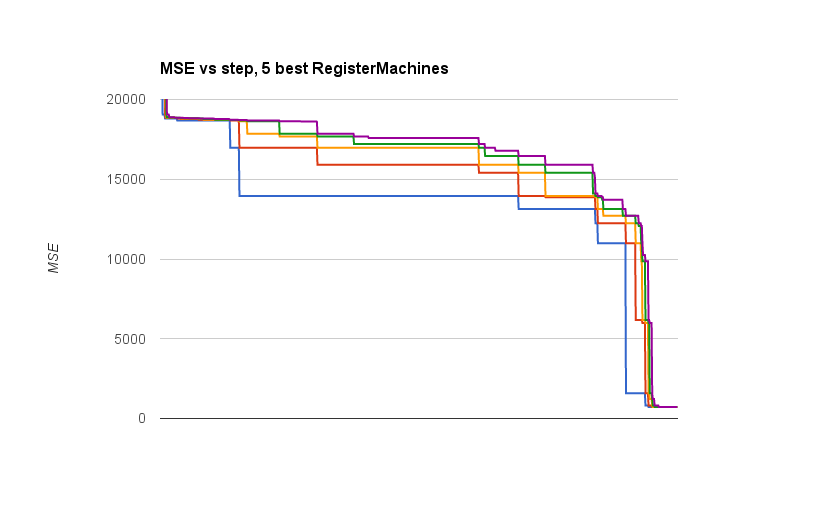
Now at the moment, my real problem is that I’ve encountered some kind of very rare error. It’s a java.lang.IndexOutOfBoundsException, it’s happening somewhere in my loop, and it’s really pissing me off.

I honestly don’t know which of my operators invoked in the loop is causing the problem, or whether it’s some edge case of executing a ProgramStep with an inappropriate index, or…. Dagnabbit, I thought I’d been pretty careful with testing.

An aside on testing

A lot of colleagues, especially those who work in Academia exclusively, ask me why I bother writing so many tests when I work, if they don’t keep me from introducing bugs. This sounds like a variant of the old, “If you’re so smart, why ain’t you rich?” sort of logic, but I’m willing to take it in stride.

I find that the question arises from those colleagues because, for whatever reason, they imagine (1) that testing slows me down when I’m writing code, an (2) that testing makes me less likely to introduce bugs. Both of those are wrong, and to be honest it shows how little they understand the incredible usefulness of constant testing. It doesn’t even have to be test-driven development (which I’m not doing here), or even test-first development. The habit of having a wide-ranging suite of automated tests running all the time while I write new code (1) speeds me up, and (2) does not make me any less likely to introduce bugs, but does make almost any bug far easier and faster to fix.

If I sense something is getting even a little more complicated than the extremely tiny amount of “design” I can hold in my head at any moment, that’s when I write a test. Recursion and iteration and fiddling with complex nested collections are all especially tricky things for me. The good old “fence post problem”—where you need to know how many times a loop will fire, but you are off by one because you counted (or didn’t count) the one at the start and the one at the end, and should have only counted one not both—is a perennial one for me.

And so that’s when I write automated tests. Whenever anything gets even slightly complicated.

The benefit, as I said, is not that the tests “make me smart” or “make the code less buggy”. I can’t imagine the mental model of a person who thinks that’s what they’re for, but nonetheless a lot of otherwise smart people seem to think that’s the argument.

No, I am experienced enough to know how stupid I can get, and to evaluate the average stupidity I tend to maintain. Both are on the high end of the scale.

The tests are there so they fail. As soon as I am just a bit too stupid, some consequence somewhere in the complex code I’ve accumulated will cause one of them to fail, and I’ll know. Not only that, but because they tend to be unit tests the particular consequence that causes the particular failed test is often obvious—that’s because unit tests are only exercising very small chunks of logic.

In this case, this weird IndexOutOfBoundsException I’m seeing, I’m no smarter or better off than anybody else. All the code I’m running was tested, but I wasn’t paranoid about it, and I certainly wasn’t using TDD.

That happens. We all cope the same way with those things. The nice thing is, as I’m trying to fix that, I will also know that I am not fucking up all the rest of the work I’ve actually covered in tests.

So, in case you were about to ask why I spend so much “extra time” on tests, ask yourself first how much “extra time” you spend changing code you’ve already written….

The Bug

Having no tests, I need to think more than usual—a painful process, probably for both of us. This thing is rare, it happens only after I’ve been running for a while, and it’s an IndexOutOfBoundsException.

There are a few places where I’m looking things up in (or writing to) collections by index. It’s a core behavior of invoke, for example, which takes a numerical index that is supposed to point to one of the items in the concatenation of :read-only and :connectors register banks. And there’s the crossover search operator, but that doesn’t feel like it’s….

Hold on right there.

Back up and think for a moment about the core of executing a program here: invoke-any-step. That picks a random item from the :program field of a RegisterMachine, and does that thing. At the beginning of the search, all the programs have 100 steps. So that shouldn’t be a problem. But… crossover combines a random number of items from both parents into one baby program… and what if that number just happens to be zero for both parents? Then there would be an empty baby program, and…. Yup, I bet that’s it.

I check something in the REPL, and confirm my suspicion. Suppose I was trying to run a rand-nth item from an empty list of program steps?

user=> (rand-nth [])
IndexOutOfBoundsException   clojure.lang.PersistentVector.arrayFor (PersistentVector.java:158)

Boom.

I think perhaps what’s happening is that an offspring is being constructed with no program steps, which is allowed as things stand right now—and, and! (that’s the sound of confirmation bias creeping in) I realize that the bug happens more often when the machines start with shorter programs. Well OK then. We can fix this! And if it crops up again later, then I’ll at least know it ain’t this problem. Here’s a revision (note the (max 1 (rand-int...))), and a test.

(defn crossover-program
  "Takes two RegisterMachines. Randomly samples some ProgramSteps from each, returning a new program combining the samples"
  [mom dad]
  (let [mom-program (:program mom)
        mom-contrib (max 1 (rand-int (count mom-program)))
        dad-program (:program dad)
        dad-contrib (max 1 (rand-int (count dad-program)))]
    (into [] (concat
      (repeatedly mom-contrib #(rand-nth mom-program))
      (repeatedly dad-contrib #(rand-nth dad-program))
      ))))

(fact "crossover-program won't ever produce an empty result"
  (let [mom (->RegisterMachine [1 1 1 1] [0 0 0] [:a :b :c :d])
        dad (->RegisterMachine [2 2 2 2] [0 0 0] [:z :y :x :w])]
    (crossover-program mom dad) => [:MOM :DAD]
    (provided (rand-int 4) => 0
              (rand-nth [:a :b :c :d]) => :MOM
              (rand-nth [:z :y :x :w]) => :DAD
              )))

New Blood

I’m tired of writing all these random numbers to STDOUT and then copying and pasting them into a CSV file. Time to write the data out straight to a file, I think. Then I should probably check whether I can scale this steady state algorithm back up to reasonable size and expect a proportional improvement.

My experience yesterday, with the design spike I didn’t show you, makes me think that probably I will need a way to introduce “new blood” into the pile of prospective answers. Either some kind of “immigration” of random RegisterMachines (but those would likely have a hard time competing with the evolved ones), or a constant background mutation of ProgramStep functions and :read-only constants. After all, I’m still playing with \(y=x+6\) here, and I suspect (from experience) that a lot of the hard part for these little guys, with their 11 random numbers, is the pressure to find a way to make the constant. Letting them have new constants might help a lot towards that goal.

Again, it’s been a few cycles since I’ve shared what’s been happening in context to my code. Here, let me share that, since it’s all self-contained in a single file, and uses Midje for the interactive testing I’ve been doing for this part.

This is what it looks like when I change the constants so that I am using a population of 100 RegisterMachine items, and evaluating all of them for 500 steps over each of 100 training cases. Which is, I still think, one hell of a lot of training cycles. But that’s what the authors seem to have wanted for \(y=sin(x)\), so it should be good enough to solve \(y=x+6\) from here.

That said, I have not implemented mutation yet. That will be in the next slide. Here’s the current code I run, right before taking a nap:

(ns artificial-chemistry.steady-state-experiment
  (:use midje.sweet)
  (:use [artificial-chemistry.core]))

;;;; implementing a simple steady state experiment interactively

(defn random-x6-case
  []
  (let [x (+ (rand 100) -50)]
    [[x] (+ x 6)]
    ))

(def x6-data
  (repeatedly 100 random-x6-case))

(def starting-pile
  (repeatedly 
    20 
    #(randomize-read-only
      (random-register-machine all-functions 11 30 100)
        100
        )))

(def scored-start-pile
  (map #(record-errors % 500 x6-data) starting-pile))

; (println 
;   (map :mse scored-start-pile))

(defn steady-state-breed-one
  "Takes a collection of RegisterMachines. Returns one new crossover product"
  [pile]
  (let [mom  (rand-nth pile)
        dad  (rand-nth pile)]
    (crossover mom dad)
    ))

; (println
;   (:mse (record-errors (steady-state-breed-one starting-pile) 20 x6-data)))

(defn steady-state-cull-one
  [pile]
  (butlast 
    (sort-by
      #(+ (:mse %) (* 100000 (:failures %)))
     (shuffle pile))))

(fact "culling removes a highest-scoring from a pile"
  (count (map :mse scored-start-pile)) => 
    (inc (count (map :mse (steady-state-cull-one scored-start-pile))))
  (map :mse scored-start-pile) =>
    (contains (map :mse (steady-state-cull-one scored-start-pile))
      :in-any-order :gaps-ok )
    )

(defn one-steady-state-step
  "Assumes the machines are scored before arriving"
  [pile steps data]
  (let [baby (record-errors (steady-state-breed-one pile) steps data)]
    (conj (steady-state-cull-one pile) baby)
    ))

(defn report-line
  [t pile]
  (do 
    (spit "steady-state-rms.csv"
          (str t ", "
            (clojure.string/join ", " (map :mse pile))
            "\n")
          :append true)
    (println
      (str t ", "
        (clojure.string/join ", " (take 5 (map :mse pile))) "..."
        ))))

(do
  (spit "steady-state-rms.csv" "")
  (loop [pile scored-start-pile
         step 0]
    (if (> step 10000)
      (report-line step pile)
      (do
        (report-line step pile)
        (recur (one-steady-state-step pile 500 x6-data)
               (inc step))
               ))))

When I wake up from my nap, we can look at the results together.

Next time: Results! And Mutants!