What can you make of this, Johnny?

This is a square:

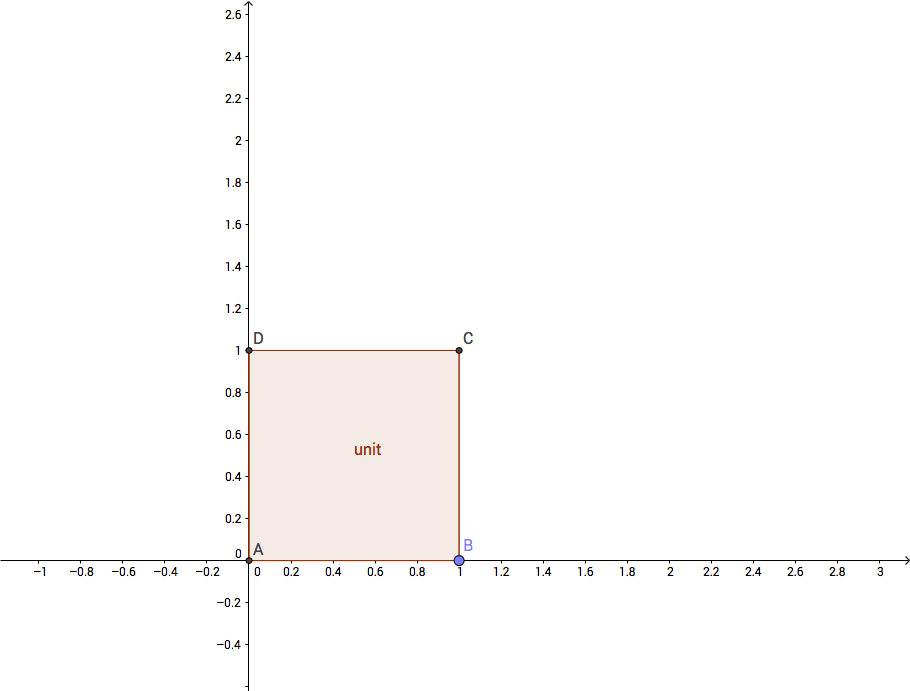
Specifically, it’s a unit square, and I drew it using this lovely open-source free-to-use online program at geogebra.org. I drew it by selecting the “Regular Polygon” tool from the polygon-drawing menu, and click-dragging an oriented line segment from the point labeled A (at (0,0)) to the point labeled B (at (1,0)). By convention in this program that is enough to completely specify a single square, uniquely: the segment drawn is the “bottom” (regardless of orientation) of a square, drawn in left-to-right direction. In other words, if I had dragged the line segment from (1,0) to (0,0), I would not have this square, but a mirror image of it, on the south side of the x-axis, since the “left” of the directed segment would have been down, not up.

Make sense? I like it.

Another thing I like about this geometry sketching system is my ability to “snap” line segments to various landmarks. I was able, for instance, to draw from exactly (0,0) to exactly (1,0), by being close enough when I drew the line or clicked the mouse or whatever it was I did. I could also draw “freehand” squares, or any other polygon, or lines, or rays, or angles, or triangles, or ellipses, or whatever, using this system. Or they too could be “magnetized” to various landmarks, when I drew them. It’s a lovely system, not least because it implements all the “traditional” geometry drawing tools (compass, straightedge, protractor, ellipse-drawing-thingie), but also a lot of other magical ones, like this polygon-drawing (for me, and for you, at the moment, square-drawing) one.

And in addition to the integer grid marks on the Cartesian plane we’re looking at, there is also an implicit new magnetic point created wherever two figures intersect. So for example, say I’ve drawn these two shaded squares ABCD and EFGH. They overlap a bit, because I just sort of slapped them down. But by using this “snap to” behavior, I can draw a third new square IJKL that is “tied” to two places where ABCD and EFGH intersect. Indeed, I drew IJKL by drag-clicking from the obvious intersection points.

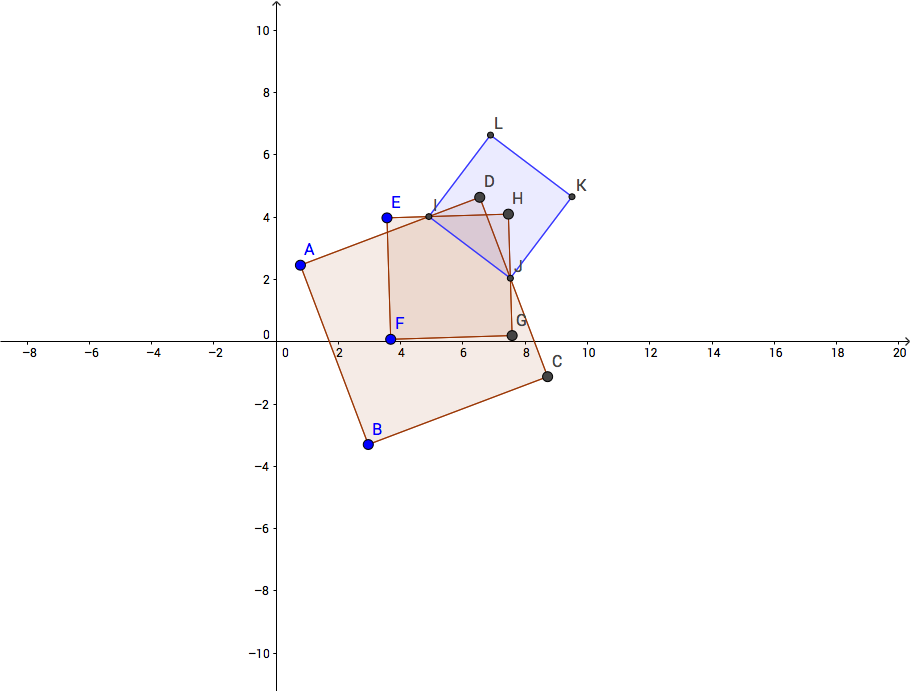
This is super fun, because IJKL is defined as being derived from—or, to use the technical geometers’ term, constructed from—the positions of the other two squares. That means, at least in this fun little exploratory system, that I can drag the defining points A and B and E and F around, and as long as the two intersection points still exist, my IJKL square will move to the correct new position. Like it was a mechanical linkage.

Sweet.

That’s not what I’m here to talk about

You can play a bunch with that lovely program. The point of me talking about the toolset, though, was to introduce a puzzle for geometric construction.

If you’ve spent any time reading recreational mathematics, or classical geometry, or if you had the right math teachers as a kid, then you’ve probably run across the idea of compass-and-straightedge constructions. Briefly, in a compass-and-straightedge construction, you can only do a few very simple stylized things:

1. You can draw a circle, with the center at a specified point, and the radius passing through some other specified point. “Specified point” here must be the intersection of two lines, the intersection of two circles, or the intersection of a line with a circle. You’re not allowed to just plop a circle anywhere, and you’re not allowed to put the center point anywhere that isn’t already the crossing-point of two figures, and you’re not allowed to draw a circle in such a way that it makes the required radial intersection point: the radius has to pass through some specific existing intersection.
2. You can draw a straight (infinite) line, as long as you do so by passing through two existing points. As with the circle, the points have to exist before you draw the line.
3. In exchange for these (severe) restrictions, you can use any point where two lines, two circles, or a line and a circle intersect as a landmark for later figures.

The point (as it were, ha ha) of a compass-and-straightedge construction problem is to arrange a sequence of new circles and lines so that, starting from some given initial pattern that has been given to you beforehand you hit a target. Some point—that is, a newly constructed intersection point—falls on a specified target point, or example when we’re constructing the corners of a pentagon. Or some line falls on in a specified target orientation, as when we’re bisecting an angle.

Note that there’s no measuring here. This “compass” can be made arbitrarily large, and the “straightedge” is perfectly straight. The trick, of course, is that we’re using algebra to determine where the intersection points are, not actual physical pencils and papers. There’s a lot of interesting mathematics here, literally millennia of work. Much of it is fascinating and convoluted, as in these fascinating animations of the construction of regular polygons.

But as flexible as the tools are, there are points (and angles) you simply cannot construct with a compass and straightedge. You might have heard of “squaring the circle”, which is constructing a square with the same area (exactly) as a given circle. You can’t do it, not with a compass and a straightedge. In the strict terms I spelled out above, I can boil this down to something like: “If I draw a circle and a line for you, and note on the line (and the circle) the two points used in constructing them, you cannot mark a second point that is exactly the right distance from one of the existing points on the line, so that a square with that side length has the same area as the circle.”

Cannot. Can’t.

Same with trisecting an angle: If I draw two lines which cross at some point, and ask you to draw a new line passing through their intersection, such that the angle between the new line and either of the others is 1/3 the original angle… you can’t. Here’s a lovely book by Underwood Dudley on this very subject. It’s fun, because it shows dozens of attempts by famous people and crackpots through the ages, many ridiculously wrong, some remarkably close, but not correct.

Indeed, I think Dudley’s book demonstrates the lengths to which human ingenuity can go, striving for an unattainable goal. The strategies, the tactics, the subtle mistakes in every case, and above all the perseverance in the face of actual proof that the task is impossible. That’s humanity, right there. There is much beauty in the ornateness of the constructions Dudley passes along. Page through the book and marvel.

And if you read it (I really do recommend it), you’ll find out something interesting. These tasks (squaring the circle, trisecting an angle) are impossible with a compass and straightedge… but they’re possible with a carpenter’s square, or with Origami paper folds, or an Archimedean spiral. Or even with a ruler and compass (where a ruler is a straightedge where you can make marks).

The toolkit makes a huge difference.

As the Wikipedia article on compass-and-straightedge constructions points out, certain numbers (and lengths) are therefore “constructible” with a given tool set, and others are not. For example, \(\sqrt{2}\) is constructible with compass-and-straightedge (as a length, relative to some given unit distance), but \(\sqrt[3]{2}\) is not.

Not in a finite number of steps, that is. You can approximate \(\sqrt[3]{2}\) with arbitrary precision only with an infinite number of constructed figures.

Whether anybody has looked at the relative convergence rates of differing algorithms… well, I don’t know about that. Yet.

Squares again

Remember the square-drawing tool in geogebra.org’s toolkit? If I have two landmark points, I can draw a full-specified square. Actually, I could pick either of two squares, because I could draw either orientation for any given two points.

Suppose I gave you that unit square I drew, before. And I told you to draw a new square. As long as I ignore any square that is coincident with an existing one, you’d have eight choices: the four squares of the same size, snug against the four edges of the first one, or the four squares whose edges are the diagonals of the first one. None of those eight new squares make a “new landmark”, though, because everywhere they cross the original is already a corner.

But, as soon as I’ve added some second square, of either sort, I can draw all kinds of new third squares. Instead of four landmark (corner) points from the original unit square, with two squares present I will have six landmarks. Again, not all fifteen possible pairs of those landmarks will produce new squares (because I’ll ignore duplicates). A few of them, not all but a few, will have edges that intersect existing edges of the first two squares.

Here’s an example. I’ve drawn one of the “diagonal moves” for the second square, and then added a third square which crosses all kinds of edges.

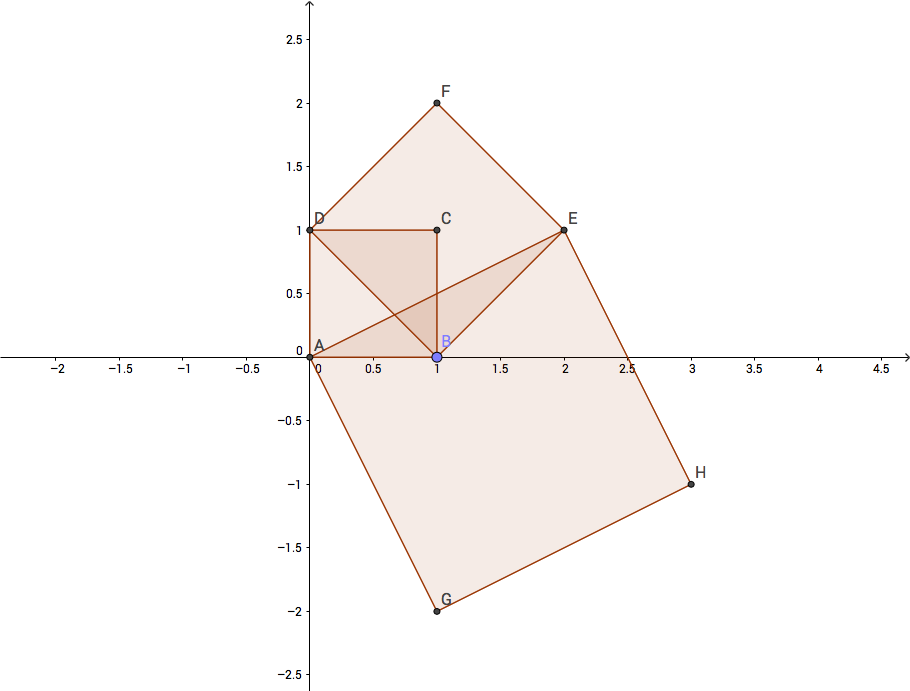
Given the initial unit square, I had 8 options for adding a second square. Having chosen the “diagonal” one, as a second square, I had… well more choices (I could count them but maybe that’s the first puzzle, or maybe it’s a bit early in the morning when I’m writing this), because we now have more landmark points (four original corners, two additional corners from the second square I drew). But having chosen as my third square the one labeled EAGH, I have not only added a couple of new corners, but have also created new intersection points where segment EA crosses segment BC and DB.

See what the combinatorics are doing, as lines start to cross? Loads more prospects than merely the ones I would have if only corners as such were available. If as a fourth square I drew one by adding a new edge DH, I would get its two new corners as well, but also three new intersections.

One is tempted, looking at a few hand-chosen examples like this one, to say things like “combinatorial explosion” and “exponential growth”, but I want to hesitate a bit. For one thing—and again I admonish you to poke at the drawing calculator interface a while and see for yourself—a lot of the “options” for drawing new squares are redundant, and produce duplicates of existing squares, which I’ve said “don’t count”. Second, because my initial setup here is a unit square and nothing else, a surprising number of the “new intersections” that occur when drawing orthogonal squares fall on top of old intersections that are already present. And finally, now and then it becomes possible to add a new square that doesn’t have any edges that cross existing ones. As a result, I have a sense that the rate at which new landmark points are added when you add arbitrary new squares “averages out” to a bit more than two new corners for every square, but that not every extra square adds new intersection points either.

I’d like to hear, frankly, what combinatorics and probability theory say will happen for any arbitrary sequence of new squares. Here’s a random process, which I’m imagining starts from the unit square by itself:

1. look at the diagram, and enumerate all possible unique “landmark points” (corners and intersections of edges)
2. pick two landmark points, \(P_1\) and \(P_2\), with uniform probability, from those present
3. draw the square \(P_1 \rightarrow P_2\)
4. repeat from 1

Now this might lead to drawing the same square over again. Frankly, I don’t know if that’s salient or not. The question for me, even before I decided whether it was important or not, would be something like, “How do the number of landmark points increase over time?” I’d generate a bunch of random samples, and count the number of landmark points in each of them, and the number of unique squares, and see what the distribution of points and squares does over, say, 10 or 20 steps.

Honestly, I’ve got no intuition about this. I think there will be quite a few new points, but then again we’re on an integer lattice to begin with, and I’ve been tricked before.

What do you think?

Counting landmark points

There’s a devil the details, here. In my counting algorithm sketch, I said “enumerate all possible unique landmark points”. It feels like this would be a challenge to my programming skills (most things are). Hell, I’d be challenged just to write an algorithm that tells me the intersection points of two arbitrary squares.

After all, two arbitrary squares might not intersect at all, either by being non-overlapping, or by being nested inside one another. Then there would be eight corners, and that’s it.

Or they could touch at one point. Which means that one square’s corner falls exactly on the boundary of the other’s (think it through and check me; I’ve been wrong a lot). Or they could coincide , or share an edge (or just part of an edge), or they could be oriented as a sort of eight-pointed-star where there are eight new intersection points….

There are a lot of possibilities, just for squares. I’m tempted to think this might be an amusing programming puzzle, a challenge on the scale of a Coding Dojo task. Maybe? Since I’m curious about squares, I expect I’ll try it out.

Before you hare off into writing your own, though, realize I’m asking the question as an exploration of how one might solve it. I’m sure there are highly efficient computational geometry packages you could download or use as libraries, and fancy scan-line algorithms that have very low computational complexity measures. Sure. Here I am simply saying, “How might you do it?” It’s about the experience of thinking a moderately small, moderately challenging thing through from start to end, not about getting the right answer.

Hitting the target

So with compass-and-straightedge constructions, we’ve already discussed the fact that there are certain distances that cannot be constructed. As I understand the result, that means that if I give you some initial circle or line, there are actually an infinitude of other circles or lines that you simply cannot construct by any finite series of rule applications.

There are plenty of circles and lines you can draw, though. That’s one of the main reasons so many people through the centuries were obsessed with squaring the circle and trisecting the angle: There are a lot of different approaches, all qualitatively different from one another, that are complex enough that you can’t visualize them all the way through to the end, and which thus might work.

This square-drawing tool, what about it? As Gary Fredericks points out in a Twitter conversation about it, it feels as if it might be a subset of things you can do with a compass and straightedge. To paraphrase where I think he’s going: you could think of my draw-a-square as a “macro” in the compass-and-straightedge low-level language. So there’s an intuition that by virtue of that relationship, maybe the square-drawing-tool has the same capacity to construct certain distances and points as compass-and-straightedge might.

I don’t know. Seriously, there’s probably a simple proof some geometer and/or algebraist (are they different?) could provide, showing that one is identical to the other, or not. I have the same intuition that Gary has—that the square-tool could be rewritten as compass-and-straightedge moves—but I wonder if I’ve also thrown something important away by limiting constructions to only that macro maneuver.

But while there is much elegance in existence proofs, I am more interested in this case in the nature of problem-solving, whether by human beings or… other processes.

So here are a series of challenges I’ve been sketching for a few weeks, which I’d like to see attempted using an abstracted square-tool construction process. I present them not because I need to know the answer (and to be frank, some may not be possible), but because I’m interested in the Circle-Squarers and Trisectors of the world.

Attempts on an impossible goal are inherently interesting. First, we all realize that it’s impossible to perfectly perform these tasks in compass-and-straightedge world, but the reason so many attempts were so highly regarded (at least by their constructors) was that all but the most egregious of them are pretty good approximations. The resulting angle might not have been algebraically 1/3 of the original, but it might have been 12/37 or 1000/2987 or whatever. And because the toolkit of compass-and-straightedge construction, limited as it sounds, provides so many paths by which to create new “landmark points”, there were many ways by which successive iterations or “subroutines” could, possibly, reach the target number more quickly than expected.

This square-tool thing I’m talking about here? What can we do with that, knowing (quite literally) nothing about what’s possible or easy? Are there iterative or recursive “functions” in the language of square-tool construction, that permit arbitrary approximation? The interesting thing about programming—to me, at least—is not that there is a path to an answer, but rather than there are so many paths to answers. Some are more “obvious” to some people (and processes), others are less “obvious” unless you (or your process) has invented some intermediate tool or component representation scheme or maneuver that others have not yet seen.

“Johnny, what do you make out of this?”

I’ll be working on these challenges myself, in the next few days. I don’t think any of them are impossible, but I could be wrong. I don’t think any of them are trivial, either, but I also could be wrong. What motivates me, though, is something I’ve been talking about the whole time. It’s the reason we explore well-understood problems in Coding Katas and Dojos, and it’s the reason there are so many crackpots who have tried to trisect an angle through the centuries, and it’s the reason I work in the discipline of genetic programming, and it’s why I make that wry smile whenever somebody says out loud that they think they can produce a useful artificial intelligence without spending the requisite twenty years spent raising it and sending it to school: The world is far more interesting than we think.

Even squares.

Tell me what you find. Especially the pterodactyls.

Some construction challenges

In all these cases, use only the square-tool I’ve been talking about. Formally:

• A “landmark point” is the corner of an existing square, or the intersection of two edges of two (or more) squares.
• Coincident edges, squares, and points are assumed to be single entities. That is, two points falling on one another exactly (measured with infinite precision, algebraically in other words) should be treated as one point. Two line segments whose ends are identical should be treated as one line segment. Two squares whose corners are identical should be treated as one square.
• The initial state for all the construction challenges is a unit square: lower left corner at (0,0) in the Cartesian plane, and upper right corner at (1,1).
• Drawing a square involves selecting an oriented pair of two different existing landmark points, call them A and B, and “dragging” an oriented edge from the A to B. The resulting square will have AB as its “base”, which is to say the area of the square will always fall to the left of ray AB. Make sense?

1. Build a square with the same center as the unit square, parallel sides, but 1/2 as large. (I think this is probably easy)
2. Build a square with the same center as the unit square, parallel sides, but 1/7 as large.
3. Build any square with side length \(\pi\), starting from the unit square.
4. Given a unit square and a “floating landmark point” located at coordinates (3,7), construct the smallest square that contains both the (entire) unit square and the landmark. Do the same for a landmark located at (5,5).
5. What is the largest (area) square you can construct in 10 moves? 20 moves? 100?
6. What is the largest proportion of the plane you can cover with squares (where overlapping areas don’t count), in 10 moves? 20 moves? 100?
7. What is the point at farthest Euclidean distance from the origin (0,0), in any direction, you can reach in 10 moves? 20 moves? 100?
8. Remembering that any identical squares are always ignored, what is the most number of “layers” of square you can stack on a single point anywhere on the plane in 10 moves? 20 moves? 100?
9. Can you draw an equilateral triangle, of any size and in any position, with the edges of three constructed squares? I find this one the hardest of all to imagine, but I’ve been surprised before.

There are of course all kinds of abstract mathematical questions you could pursue, too. For instance, it might be interesting to consider whether there are particular values of \(1/n\) scaled squares you cannot construct, centered on (1/2,1/2). Or whether there are particular points on the plane you cannot exactly place a landmark point on (which I suspect is the case). Or whether, as Gary Fredericks has suggested above, this is the “same” in any sense as compass-and-straightedge construction, or whether it’s got more or less flexibility—group theory stuff I don’t personally understand very well.

There is also a pile of computational geometry stuff one could get bogged down in: Do you want to use or build an algebraic solver for exact symbolic calculations of points? Or do you want to use an arbitrary-precision floating point type? Or something else? Do you want to generalize to rectangles? Arbitrary polygons? I didn’t ask, but you might already be wondering about whether equilateral triangles or regular pentagons have the same characteristics as my square-tool does.

And that is the point. Explore. Tell me (and other people) what you find.

It’s the looking to see that’s the interesting part.