Mutating Register Machines
Draft of 2016.08.02
May include: GP ↘ AI ↗ learning in public ↖ &c.
Continued from Breeding Register Machines
Back again, after a good nap. Here’s what happened while I was sleeping, and since:
- The search I was running (on the fast desktop computer, because this is not an efficient algorithm for fitting curves to lines, and it’s not intended to be!) suddenly jumped from an
:mseof about27000down to an:mseof about1800. That was a huge drop. And when I woke up and saw the numbers change in theSTDOUTspew that had collected, that’s when I realized at least four different things:- Oops! That’s not the mean squared error, it’s the summed squared error. My bad. It’s not normalized by the number of training cases at all
- There really does need to be a source of variation, besides just crossover of the original numeric constants in the
:read-onlyregisters, and the:programsteps. The population ends up getting bottlenecked—basically becoming inbred—surprisingly quickly. - In the original paper, the authors actually say they evaluate their
RegisterMachinescores against a random subset of the training cases. I decide to slightly modify the code so that it samples 50 cases for each evaluation, from the 100 cases I’ve built originally - The real kicker: I totally forgot to write the “best” machine found to disk. So even though the scores dropped substantially, there was literally no way to interrogate the process and look at what was happening inside the program.
The last one was enough justification to halt the run in progress. The third one actually speeds it up a bit, too. I decide to just keep using “summed squared error”, because what’s a divisor among friends? And as for the variation: MUTATE NOW.
And then there’s one huge thing to worry about, once things get going for real. How do I tell what one of these RegisterMachine things actually does? They’re crazy. They make no sense. I’ll have to graph them, maybe.
Mutate now!
Just to bring us all up to speed (this is the sixth entry in this narrative, after all, and people might arrive via Google or something), here’s the code I’m running at the moment for this experiment, after changing the way :error is calculated, and also after including a way to report the “best” at the end. Recall that this is an extremely simple steady state evolutionary algorithm. I’m taking two “parents”, chosen uniformly from the population, making a single offspring by recombining them (according to the algorithm described in the original book chapter), and testing each one by running it for 500 updates, after being initialized with one of 50 randomly-chosen training cases, trying to fit \(y=x+6\):
(ns artificial-chemistry.steady-state-experiment (:use midje.sweet) (:use [artificial-chemistry.core])) ;;;; implementing a simple steady state experiment interactively (defn random-x6-case [] (let [x (+ (rand 100) -50)] [[x] (+ x 6)] )) (def x6-data (repeatedly 100 random-x6-case)) (def starting-pile (repeatedly 100 #(randomize-read-only (random-register-machine all-functions 11 30 100) 100 ))) (def scored-start-pile (map #(record-errors % 500 (take 50 (shuffle x6-data))) starting-pile)) ; (println ; (map :mse scored-start-pile)) (defn steady-state-breed-one "Takes a collection of RegisterMachines. Returns one new crossover product" [pile] (let [mom (rand-nth pile) dad (rand-nth pile)] (crossover mom dad) )) ; (println ; (:mse (record-errors (steady-state-breed-one starting-pile) 20 x6-data))) (defn steady-state-cull-one [pile] (butlast (sort-by #(+ (:mse %) (* 100000 (:failures %))) (shuffle pile)))) (fact "culling removes a highest-scoring from a pile" (count (map :mse scored-start-pile)) => (inc (count (map :mse (steady-state-cull-one scored-start-pile)))) (map :mse scored-start-pile) => (contains (map :mse (steady-state-cull-one scored-start-pile)) :in-any-order :gaps-ok ) ) (defn one-steady-state-step "Assumes the machines are scored before arriving" [pile steps data] (let [baby (record-errors (steady-state-breed-one pile) steps data)] (conj (steady-state-cull-one pile) baby) )) (defn report-line [t pile] (do (spit "steady-state-rms.csv" (str t ", " (clojure.string/join ", " (map :mse pile)) "\n") :append true) (println (str t ", " (clojure.string/join ", " (take 5 (map :mse pile))) "..." )))) (defn report-best [t pile] (do (spit "steady-state-bests.csv" (str t ", " (pr-str (second pile)) "\n") :append true) )) (do (spit "steady-state-rms.csv" "") (loop [pile scored-start-pile step 0] (if (> step 10000) (report-best step pile) (do (report-line step pile) (recur (one-steady-state-step pile 500 (take 50 (shuffle x6-data))) (inc step)) ))))
Now, the original book chapter was running a completely different generational search algorithm from the one I’m running, an I’ll happily implement that shortly. Most of the parts are more or less the same as what I have now, anyway. In their description, they say they mutate the numerical values in :read-only registers using Gaussian deviates, with standard deviation 1.0.
OK, I can do that. Or at least somebody can.
Specifically, this guy can. I add the library dependency to the project, and load it into the artificial-chemistry.core namespace. I want it there, since I’m going to want to add a mutate-registers function right below my crossover-registers function in the library.
Here’s the new namespace declaration:
(ns artificial-chemistry.core (:require [clojure.math.numeric-tower :as math] [roul.random :as rr]))
And here is the function and its test:
(defn crossover-registers "Takes two RegisterMachines. Constructs a new `:read-only` vector by sampling from the two with equal probability." [mom dad] (map #(rand-nth [%1 %2]) (:read-only mom) (:read-only dad))) (fact "mutate-registers" (let [rm (->RegisterMachine [1 1 1 1] [] [])] (:read-only (mutate-registers rm 0.0)) => (:read-only rm) (:read-only (mutate-registers rm 1.0)) =not=> (contains 1) (:read-only (mutate-registers rm 1.0)) => [99 99 99 99] (provided (rr/rand-gaussian 1 1.0) => 99) ))
As for mutating the :program, I’ve re-read the paper’s version, and I have to say it’s surprisingly unsatisfying. I may give it a try, but come on: I’m here to add diversity, not twiddle the details of who is connected to whom. These are “programs” that are run in random order, and if you’re going to make a change it had better be a substantial one if that diversity is going to be useful and/or carried forward with all the layered sampling.
So here’s my version of mutate-program: With probability p, change each :program step to a completely new random-program-step result. Just jam that new one in there.
(defn mutate-program "Tkes a RegisterMachine, and a probability of mutation. Each step of the `:program` is changed with that probability to a completely new `random-program-step` result." [rm prob] (let [old-program (:program rm) ro-count (count (:read-only rm)) cxn-count (count (:connectors rm))] (assoc rm :program (map #(if (< (rand) prob) (random-program-step all-functions ro-count cxn-count) %) old-program)) )) (fact "mutate-program" (let [rm (->RegisterMachine [1 2] [1 2] [:a :b :c])] (:program (mutate-program rm 0.0)) => (:program rm) (:program (mutate-program rm 1.0)) =not=> (contains :a) (map class (:program (mutate-program rm 1.0))) => [artificial_chemistry.core.ProgramStep artificial_chemistry.core.ProgramStep artificial_chemistry.core.ProgramStep] (map :args (:program (mutate-program rm 1.0))) => [ [1 2] [3 1] [2 3]] (provided (rand-int 4) =streams=> (cycle [1 2 3]) (rand-int 2) => 1 (rand-nth all-functions) => (first all-functions)) ))
Then, as with crossover, there’s a single function to bring it all together:
(defn mutate "Takes a RegisterMachine and a probability, and changes both the `:read-only` registers and the program steps with that probability." [rm prob] (-> rm (mutate-registers , prob) (mutate-program , prob)))
Who should I apply it to, though? The baby constructed by crossover is already pretty much at a disadvantage. Maybe I could mutate the “best” one, and add that to the population as well? In other words, make one new offspring by crossover, and another by mutating the best-scoring one.
That will entail a slight change in the algorithm. I’ll add two new RegisterMachines in each cycle, so I’ll need to cull two as well. Here’s what I decide on, for now:
(defn one-steady-state-step "Assumes the machines are scored before arriving" [pile steps data] (let [baby (record-errors (steady-state-breed-one pile) steps data) mute (record-errors (mutate (rand-nth pile) 0.05) steps data)] (-> pile steady-state-cull-one (conj , mute) steady-state-cull-one (conj , baby) )))
That is:
- remove the worst-scoring machine
- take one
RegisterMachineat random, and add a mutant of it (prob= 0.05 per gene or register) - remove the worst-scoring machine
- pick two random parents, and produce a
crossoveroffspring, and add it to the pile
I’ll try that a few times, with full data and 500 steps of evaluation, just to see what comes of it. And while that’s running, we should both be trying to figure out how to draw what these programs look like. In case we get something that actually works, for example.
How they’re doing
Not so good, as it happens:
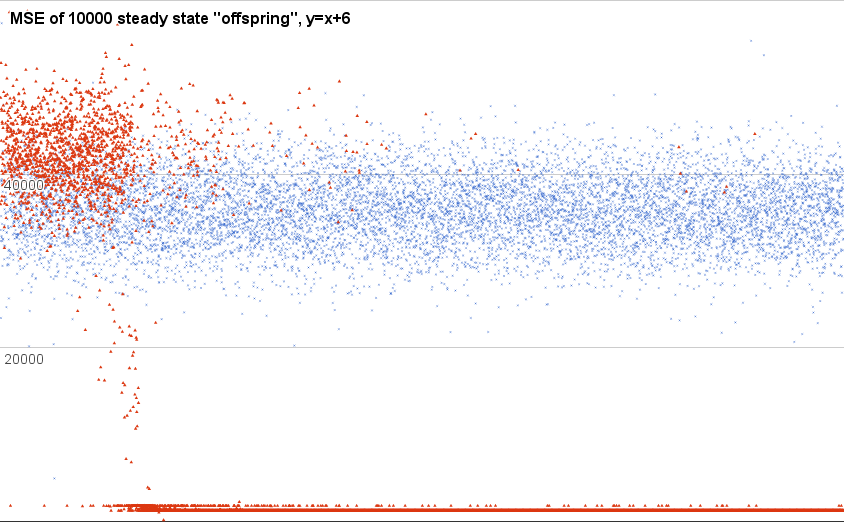
This is a plot of just the new ones. That is, the “offspring” produced by breeding two random-chosen parents. The blue X shaped points are from one run of that little dumb steady-state algorithm I posted above, and the red triangles are from another run.
Also, this chart is cropped on the y axis; there are loads of super-high (including many Infinity) scores along the way. This is just the “fine detail” down near whatcha might call “not-totally-stupid” territory.
As you can see, over time (the x axis, here, is the order of creation), the blue time-series is just dawdling around, with no obvious change in population behavior. The red triangle run (chosen because it was the only other qualitatively different sort of behavior, besides that you see in the first) starts off about the same, but then somebody stumbles on some kind of trick—the score for the “best” during most of this time is 1250.0, implying that it is exactly 25.0 points off for each of the 50 training cases.
I’m pleased to see something is possible here, but I literally don’t know how to interpreter this information. I don’t have a sense, for example, of how variable the behavior of one single RegisterMachine might be. Is the scatter of scores in the blue X run due to variation from different programs with different steps, or is it within the range of variability one would see if a single program were run a bunch of times?
The object lesson: Every “what can it hurt?” decision you make when you’re building an evolutionary search system can have consequences and interactions with all kinds of other design decisions.
I think I should probably implement something closer to the original paper’s generational algorithm, and see what that does. Luckily, most of the tools needed are already on hand.
Generational GP
The fundamental distinction between a steady state and a generational evolutionary algorithm is relatively easy to describe, though the dynamics of search (and appropriateness) are surprisingly variable and problem-specific: In steady state search, we make one (or a few) new answers, and replace somebody in the pile with those; in a generational algorithm, we make a whole new pile of new ones, and throw away the old pile.
One question left unanswered by the chapter I’m working from is what they do for a selection algorithm. In the steady state loop I’ve been working on so far, I’ve been using an approach that’s unusual in the literature: throwing the worst-scoring individual away. For one reason or another (and there’s a whole long pile of engineering criticism I should write about the historical reasons and the disciplinary consequences of this decision), almost all evolutionary algorithms papers use a weird sort of “positive selection” in their work: the best-scoring individuals are used to produce offspring. This is… well, it’s complicated, but it’s a conflation of several different understandings of biological “fitness” and selection, filtered through a metaphor or two, and layered under with years of disciplinary habit.
But there’s no mention whatsoever of the selection algorithm used in this paper. There’s a sort of aside, in which they say that one of the best-scoring individuals is “lost”, so that’s a bit of a clue. Not enough to make a firm prediction from, though.
So here’s my plan for a new algorithm with which I can compare this first, not-very-good one, given the paucity of information and the tools I have on hand:
- make and score a pile of random individuals
- make and score an equal-sized pile of their offspring (by crossover and mutation)
- cull the worst-scoring half of that pile
Both hands tied behind their backs
You know, I wrote that algorithm (a final version below; bear with me a moment more), and the surprising ineptitude of the process to find and take advantage of improved “programs” was bugging me.
So I found a bug.
This is, ironically, exactly one of those things I just said in the doubly-previous section was something to watch out for. Here’s the narrative arc in numbered-list form:
- I read in the paper that they used 11
:read-onlyregisters, 30:connectors, and 100-step programs. I decide to implement myRegisterMachinestuff with those same parameters, because why not? - I read in the paper that they initialized the search algorithm with programs that had 100
ProgramStepentries (again, using my nomenclature here), so that’s what I did too! Hey, this reading thing is pretty handy! - The paper says they evaluated the performance of their programs for 500 steps, because that’s five times the length of the program, and they say that they always run the programs a number of steps equal to five times the length of the program. So I make it so all my
RegisterMachinetesting uses 500 cycles of updating, every time, hard-coded as a Magic Number. Note that one for a sec, OK? - The paper says they used a weird crossover technique where they sample somewhere between
0and the number of steps in a machine’s:program, so the number of steps in the programs can change stochastically. It’s weird, but I do that too. - When I run my steady state algorithm—which is even simpler than the one they describe in the paper—it solves the problem I give it very, very badly. Like I am appalled and embarrassed at how crappy this algorithm, which has served me well and faithfully for many a year, is doing on this damned simple problem. I think to myself, “There must be numerous simple solutions to this problem! How can it possibly be that these
RegisterMachinethings are so hard to evolve, even by this bog-simple algorithm I trust?!”
Which is your cue to yell at the stage: “You idiot, you didn’t do what it said in the paper!” True enough, audience. True enough.
The object lesson: Every “what can it hurt?” decision you make when you’re building an evolutionary search system can have consequences and interactions with all kinds of other design decisions.
A RegisterMachine runs by picking random steps and doing those. If it has 100 imperative items in its program, then running it for 500 steps will do a fair job at picking some of those, but to be frank, it’s not as even a selection as you think. Rather than writing a simulator, I asked Wolfram Alpha and it sure looks like there will be some steps that are run not at all, and several that are run 10 or more times each.
Hey look, I wonder what happens when I run a 50-function program for 500 steps? Oh wow, all of the steps run at least 4-5 times each, and a bunch of them run 15+ times.
Here’s what I noticed, when I plotted those data above that show one time-series where nothing changes, and another where it “discovers” a low-score variation that takes over quickly: the low-scoring one is small. Like 10-20 functions small.
And this is where you ask, pointedly: How much stuff happens when you run a 20-function program for 500 steps?
A: Every function is executed at least 10 times, in the samples I’ve done; some are executed as many as 40.
It’s an interesting trade-off, and a good example of just the sort of thing I was saying earlier about unintended consequences and interactions. If I have a long program, and run it 500 steps, then I have a good chance of sampling all the steps at least once, and that sort of program—once it’s well-tuned by evolution or intentional design—can leverage a complicated and function graph with many components to devote just enough effort to answering the problem, while burning off all the excess cycles doing stuff that doesn’t really matter. Meanwhile a smaller program, one that has only a few dozen, or even one dozen, functions, when that runs 500 steps, all those steps will happen lots of times.
But if I had read the paper right the first time, and actually written my code so that every evaluation was permitted only five steps for each function in its program… that’s different. I can’t even say how. It’s just different enough that now—now that I’ve made the change—it works. Much better.
Solved \(y=x+6\) (to within 0.001 of the target, 0.0, which is good enough for me), both in the generational and the steady-state algorithms. It even solves that problem when I start the population with 100-function programs, now that I’ve fixed the bug and evaluate all programs for \(5\times\) the number of functions they contain.
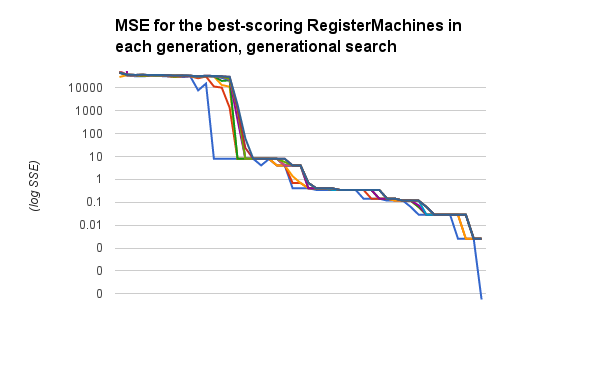
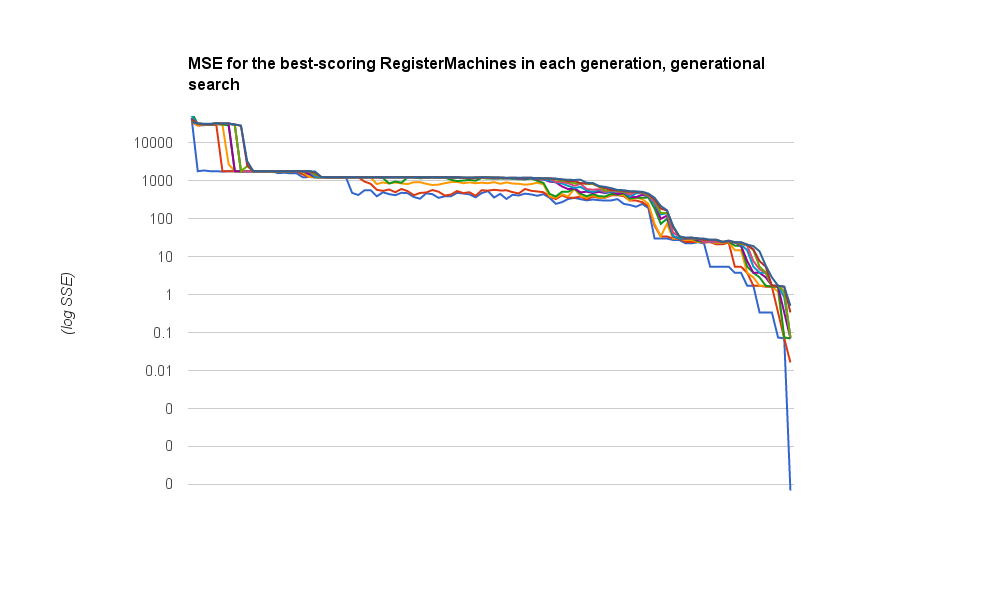
I want to run this overnight (a few times) on the \(y=sin(x)\) problem, because I have yet to see that solved at all. But let me show you the difference, now, in how quickly and readily these algorithms are working on \(y=x+6\); you can compare somewhat with the plot above, though I’m plotting something different here.
Here are the :mse scores for the best ten RegisterMachines in the population, traced over time. Now these steps are generations, so at least a hundred new individuals have been bred between each data point along the x axis. But the trend is pretty obvious, even so:
Oh, and here’s the simple code I used for the generational search:
(defn one-generational-step "Assumes machines are scored before arriving; shuffles and samples data for each evaluation" [pile scale-factor data] (let [n (count pile)] (into [] (-> pile (into , (generational-breed-many pile n)) (score-pile , scale-factor data) (generational-cull-many , n) )))) (do (spit "generational-rms.csv" "") (loop [pile scored-start-pile step 0] (if (or (> step 500) (< (:mse (first pile)) 0.001)) (do (report-line "generational-rms.csv" step pile) (report-best "generational-rms-best.csv" step pile)) (do (report-line "generational-rms.csv" step pile) (recur (one-generational-step pile 5 x6-data) (inc step)) ))))
In other words, in each “generational step” I construct the same number of babies as there are population members already, picking all the parents with uniform probability (ignoring their scores). Then I score everybody—even the parents who have already been scored—and sort by that weighted :mse-plus-10000-per-:failure score I used before, and then throw away the worst half.
There are also several other changes, mainly related to the bug I just told you about. Tomorrow I’ll start with a full disclosure, because I want to refactor it quite a bit more, and actually integrate this exploratory code into the main library for this project.
For tomorrow
Now that I have actually evolved a RegisterMachine that does “what I asked” (I am skeptical, in the sense of having one hell of a lot of experience with genetic programming), I’d like to look at how the “best” one works. But I’m a little bit frustrated, because clearly I’ve not been as “mindful” as I like to imagine I could be. I carefully saved the “best” in a file, every time a search finishes with a low enough score, or times out. But here’s the sort of data in the file:
97, #artificial_chemistry.core.RegisterMachine{:read-only (-37.998084822111196 93.10616921481831 -83.42130518386197 41.66452060110288 37.97987432544676 -11.487022761164258 98.73810583953534 -37.572432421149095 64.37549377628864 12.367799356586755 81.53610066962965), :connectors [0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0], :program (#artificial_chemistry.core.ProgramStep{:function #object[clojure.core$_PLUS__SINGLEQUOTE_ 0x6c9b6332 "clojure.core$_PLUS__SINGLEQUOTE_@6c9b6332"], :args [11 14], :target 29} #artificial_chemistry.core.ProgramStep{:function #object[clojure.core$_PLUS__SINGLEQUOTE_ 0x6c9b6332 "clojure.core$_PLUS__SINGLEQUOTE_@6c9b6332"], :args [36 3], :target 27} #artificial_chemistry.core.ProgramStep{:function #object[artificial_chemistry.core$pow 0x4889fbba "artificial_chemistry.core$pow@4889fbba"], :args [30 19], :target 21} #artificial_chemistry.core.ProgramStep{:function #object[clojure.core$_PLUS__SINGLEQUOTE_ 0x6c9b6332 "clojure.core$_PLUS__SINGLEQUOTE_@6c9b6332"], :args [11 14], :target 29} #artificial_chemistry.core.ProgramStep{:function #object[artificial_chemistry.core$pdiv 0x572db5ee "artificial_chemistry.core$pdiv@572db5ee"], :args [38 1], :target 3} #artificial_chemistry.core.ProgramStep{:function #object[artificial_chemistry.core$rm_and 0x31ab75a5 "artificial_chemistry.core$rm_and@31ab75a5"], :args [17 5], :target 8} #artificial_chemistry.core.ProgramStep{:function #object[artificial_chemistry.core$pow 0x4889fbba "artificial_chemistry.core$pow@4889fbba"], :args [30 19], :target 21} #artificial_chemistry.core.ProgramStep{:function #object[clojure.core$_PLUS__SINGLEQUOTE_ 0x6c9b6332 "clojure.core$_PLUS__SINGLEQUOTE_@6c9b6332"], :args [11 14], :target 29} #artificial_chemistry.core.ProgramStep{:function #object[artificial_chemistry.core$rm_or 0x2dec57c5 "artificial_chemistry.core$rm_or@2dec57c5"], :args [22 36], :target 17} #artificial_chemistry.core.ProgramStep{:function #object[artificial_chemistry.core$pow 0x4889fbba "artificial_chemistry.core$pow@4889fbba"], :args [30 19], :target 21} #artificial_chemistry.core.ProgramStep{:function #object[clojure.core$_STAR__SINGLEQUOTE_ 0x31e9d94f "clojure.core$_STAR__SINGLEQUOTE_@31e9d94f"], :args [3 9], :target 25} #artificial_chemistry.core.ProgramStep{:function #object[artificial_chemistry.core$pow 0x4889fbba "artificial_chemistry.core$pow@4889fbba"], :args [2 13], :target 21} #artificial_chemistry.core.ProgramStep{:function #object[clojure.core$_PLUS__SINGLEQUOTE_ 0x6c9b6332 "clojure.core$_PLUS__SINGLEQUOTE_@6c9b6332"], :args [20 30], :target 10} #artificial_chemistry.core.ProgramStep{:function #object[clojure.core$_PLUS__SINGLEQUOTE_ 0x6c9b6332 "clojure.core$_PLUS__SINGLEQUOTE_@6c9b6332"], :args [11 14], :target 29} #artificial_chemistry.core.ProgramStep{:function #object[clojure.core$_PLUS__SINGLEQUOTE_ 0x6c9b6332 "clojure.core$_PLUS__SINGLEQUOTE_@6c9b6332"], :args [15 39], :target 28} #artificial_chemistry.core.ProgramStep{:function #object[clojure.core$_STAR__SINGLEQUOTE_ 0x31e9d94f "clojure.core$_STAR__SINGLEQUOTE_@31e9d94f"], :args [40 31], :target 15} #artificial_chemistry.core.ProgramStep{:function #object[artificial_chemistry.core$rm_or 0x2dec57c5 "artificial_chemistry.core$rm_or@2dec57c5"], :args [22 36], :target 17} #artificial_chemistry.core.ProgramStep{:function #object[artificial_chemistry.core$rm_or 0x2dec57c5 "artificial_chemistry.core$rm_or@2dec57c5"], :args [36 26], :target 12} #artificial_chemistry.core.ProgramStep{:function #object[clojure.core$_PLUS__SINGLEQUOTE_ 0x6c9b6332 "clojure.core$_PLUS__SINGLEQUOTE_@6c9b6332"], :args [36 3], :target 27} #artificial_chemistry.core.ProgramStep{:function #object[clojure.core$__SINGLEQUOTE_ 0x4987142d "clojure.core$__SINGLEQUOTE_@4987142d"], :args [3 10], :target 21} #artificial_chemistry.core.ProgramStep{:function #object[artificial_chemistry.core$pow 0x4889fbba "artificial_chemistry.core$pow@4889fbba"], :args [30 19], :target 21} #artificial_chemistry.core.ProgramStep{:function #object[artificial_chemistry.core$rm_and 0x31ab75a5 "artificial_chemistry.core$rm_and@31ab75a5"], :args [17 11], :target 21} #artificial_chemistry.core.ProgramStep{:function #object[clojure.core$_STAR__SINGLEQUOTE_ 0x31e9d94f "clojure.core$_STAR__SINGLEQUOTE_@31e9d94f"], :args [23 2], :target 11} #artificial_chemistry.core.ProgramStep{:function #object[clojure.core$_PLUS__SINGLEQUOTE_ 0x6c9b6332 "clojure.core$_PLUS__SINGLEQUOTE_@6c9b6332"], :args [16 18], :target 22} #artificial_chemistry.core.ProgramStep{:function #object[artificial_chemistry.core$rm_or 0x2dec57c5 "artificial_chemistry.core$rm_or@2dec57c5"], :args [22 36], :target 17} #artificial_chemistry.core.ProgramStep{:function #object[artificial_chemistry.core$pdiv 0x572db5ee "artificial_chemistry.core$pdiv@572db5ee"], :args [29 28], :target 5} #artificial_chemistry.core.ProgramStep{:function #object[artificial_chemistry.core$pow 0x4889fbba "artificial_chemistry.core$pow@4889fbba"], :args [33 4], :target 18} #artificial_chemistry.core.ProgramStep{:function #object[clojure.core$_PLUS__SINGLEQUOTE_ 0x6c9b6332 "clojure.core$_PLUS__SINGLEQUOTE_@6c9b6332"], :args [11 14], :target 29}), :error-vector [0.017980157696413812 0.017980157696413812 0.017980157696413812 0.017980157696412036 0.017980157696413812 0.017980157696413812 0.017980157696413812 0.017980157696412036 0.017980157696413812 0.017980157696413812 0.017980157696413812 0.01798015769641026 0.017980157696413812 0.017980157696412036 0.017980157696412036 0.017980157696413812 0.017980157696412036 0.017980157696412036 0.017980157696412036 0.017980157696412036 0.017980157696413812 0.01798015769641026 0.017980157696413812 0.017980157696412036 0.017980157696412036 0.017980157696412036 0.017980157696413812 0.017980157696412036 0.017980157696413812 0.017980157696413812 0.017980157696413812 0.01798015769641026 0.017980157696413812 0.017980157696413812 0.017980157696413812 0.017980157696412036 0.01798015769641026 0.017980157696413812 0.017980157696413812 0.01798015769641026 0.017980157696413812 0.017980157696412036 0.017980157696412036 0.017980157696413812 0.017980157696413812 0.017980157696413812 0.017980157696412036 0.017980157696413812 0.01798015769641026 0.017980157696413812], :mse 0.016164303539393663, :failures 0}
I’m good with some of this. For example, I like seeing :mse 0.016164303539393663 and :failures 0 right there. And I actually already know a lot about how this guy works from looking at
:error-vector [0.017980157696413812 0.017980157696413812 0.017980157696413812 0.017980157696412036 0.017980157696413812 0.017980157696413812 0.017980157696413812 0.017980157696412036 0.017980157696413812 0.017980157696413812 0.017980157696413812 0.01798015769641026 0.017980157696413812 0.017980157696412036 0.017980157696412036 0.017980157696413812 0.017980157696412036 0.017980157696412036 0.017980157696412036 0.017980157696412036 0.017980157696413812 0.01798015769641026 0.017980157696413812 0.017980157696412036 0.017980157696412036 0.017980157696412036 0.017980157696413812 0.017980157696412036 0.017980157696413812 0.017980157696413812 0.017980157696413812 0.01798015769641026 0.017980157696413812 0.017980157696413812 0.017980157696413812 0.017980157696412036 0.01798015769641026 0.017980157696413812 0.017980157696413812 0.01798015769641026 0.017980157696413812 0.017980157696412036 0.017980157696412036 0.017980157696413812 0.017980157696413812 0.017980157696413812 0.017980157696412036 0.017980157696413812 0.01798015769641026 0.017980157696413812]
Somehow he’s managed to provide a robust result of \(y=x+6+\epsilon\), for some small \(\epsilon\) because all he’s got is a few constants to work with. And I can see those constants, too:
:read-only (-37.998084822111196 93.10616921481831 -83.42130518386197 41.66452060110288 37.97987432544676 -11.487022761164258 98.73810583953534 -37.572432421149095 64.37549377628864 12.367799356586755 81.53610066962965)
But what are his program steps?
Some are the function "clojure.core$_STAR__SINGLEQUOTE_@31e9d94f", which I assume is '*'. And some are "clojure.core$_PLUS__SINGLEQUOTE_@6c9b6332". Luckily, I can even make out my own library’s functions among the gibberish, like "artificial_chemistry.core$rm_or@2dec57c5" must be my rm-or function.
Then there’s this one really weird one: #object[clojure.core$__SINGLEQUOTE_ 0x4987142d "clojure.core$__SINGLEQUOTE_@4987142d". Somehow… a Clojure 'quote function has been bound to a RegisterMachine function? How? What have I done now? That’s another mysterious bug to fix tomorrow. I suspect it might be some weirdness with the -' function, since I see none of those. But who knows?
Tomorrow, I’ll sort it out. It’s been a a long day already, and now that things are working I can collect some data on the real problem(s).
Here’s a rough translation of this dude’s program into something a bit more legible, by the power of Find-and-Replace:
:program ( #artificial_chemistry.core.ProgramStep{ :function "+", :args [11 14], :target 29} #artificial_chemistry.core.ProgramStep{ :function "+", :args [36 3], :target 27} #artificial_chemistry.core.ProgramStep{ :function "POW", :args [30 19], :target 21} #artificial_chemistry.core.ProgramStep{ :function "+", :args [11 14], :target 29} #artificial_chemistry.core.ProgramStep{ :function "pdiv", :args [38 1], :target 3} #artificial_chemistry.core.ProgramStep{ :function "AND", :args [17 5], :target 8} #artificial_chemistry.core.ProgramStep{ :function "POW", :args [30 19], :target 21} #artificial_chemistry.core.ProgramStep{ :function "+", :args [11 14], :target 29} #artificial_chemistry.core.ProgramStep{ :function "OR", :args [22 36], :target 17} #artificial_chemistry.core.ProgramStep{ :function "POW", :args [30 19], :target 21} #artificial_chemistry.core.ProgramStep{ :function "*", :args [3 9], :target 25} #artificial_chemistry.core.ProgramStep{ :function "POW", :args [2 13], :target 21} #artificial_chemistry.core.ProgramStep{ :function "+", :args [20 30], :target 10} #artificial_chemistry.core.ProgramStep{ :function "+", :args [11 14], :target 29} #artificial_chemistry.core.ProgramStep{ :function "+", :args [15 39], :target 28} #artificial_chemistry.core.ProgramStep{ :function "*", :args [40 31], :target 15} #artificial_chemistry.core.ProgramStep{ :function "OR", :args [22 36], :target 17} #artificial_chemistry.core.ProgramStep{ :function "OR", :args [36 26], :target 12} #artificial_chemistry.core.ProgramStep{ :function "+", :args [36 3], :target 27} #artificial_chemistry.core.ProgramStep{ :function #object[clojure.core$__SINGLEQUOTE_ 0x4987142d "clojure.core$__SINGLEQUOTE_@4987142d"], :args [3 10], :target 21} #artificial_chemistry.core.ProgramStep{ :function "POW", :args [30 19], :target 21} #artificial_chemistry.core.ProgramStep{ :function "AND", :args [17 11], :target 21} #artificial_chemistry.core.ProgramStep{ :function "*", :args [23 2], :target 11} #artificial_chemistry.core.ProgramStep{ :function "+", :args [16 18], :target 22} #artificial_chemistry.core.ProgramStep{ :function "OR", :args [22 36], :target 17} #artificial_chemistry.core.ProgramStep{ :function "pdiv", :args [29 28], :target 5} #artificial_chemistry.core.ProgramStep{ :function "POW", :args [33 4], :target 18} #artificial_chemistry.core.ProgramStep{ :function "+", :args [11 14], :target 29})
Mysteries to be solved tomorrow:
- Where did that
SINGLEQUOTEcome from? - How can I visualize the actual behavior of this dude, and especially how does he produce exactly the \(y=x+6+\epsilon\) answer he does, running these 28 functions over 140 uniform random samples? I still can’t figure that one out.
- I showed you generational and steady-state results above. As I mentioned the steady state algorithm is recording data every time a new
RegisterMachineis constructed, while the generational one is not (yet) recording every individual that it constructs and evaluates. So the behavior of a generational algorithm with 100 generations of 100 individuals each, should technically be compared against a steady-state algorithm that has had an opportunity to also evaluate 10000 new individuals. I’m not doing that here, but I should.
No, seriously… SINGLEQUOTE??
I’ll show you the code I’m running (which is greatly improved by refactoring and finding these little bugs and misreadings) tomorrow. After I find out where that SINGLEQUOTE arrived from.
Next time: SINGLEQUOTE?!